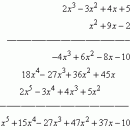ЧИСЛО
Понятие числа в математике может относиться к объектам различной природы: натуральным числам, используемым при счете (положительным целым числам 1, 2, 3 и т.д.), числам, являющимся возможными результатами (идеализированных) измерений (это такие числа, как 2/3, 
, – их называют действительными числами), отрицательным числам, мнимым числам (скажем, к 
) и к другим более абстрактным классам чисел, используемым в высших разделах математики (например, к гиперкомплексным и трансфинитным числам). Число необходимо отличать от его символа, или обозначения, которое его представляет. Мы рассмотрим логические отношения между различными классами чисел.
Элементарная арифметика оперирует с положительными целыми числами и нулем, с дробями, в известной мере с положительными действительными числами, такими как , и иногда с отрицательными действительными числами. Более сложные действия над отрицательными и мнимыми числами обычно принято относить к компетенции алгебры. Правила, осваиваемые при изучении арифметики, применимы без каких-либо ограничений только к положительным действительным числам, поэтому некоторые действия, производимые над более общими классами чисел, часто кажутся загадочными, например
Такие загадки легко разрешаются, если принять во внимание, что различные классы чисел имеют совершенно различный смысл; хотя у них достаточного много общего, чтобы их всех можно было называть числами, не следует думать, что все они будут удовлетворять одним и тем же правилам.
Положительные целые числа.
Хотя мы все усваиваем положительные целые числа (1, 2, 3 и т.д.) в раннем детстве, когда вряд ли приходит в голову задумываться об определениях, тем не менее такие числа могут быть определены по всем правилам формальной логики. Строгое определение числа 1 заняло бы не один десяток страниц, а формула типа 1 + 1 = 2, если записать ее во всех подробностях без каких-либо сокращений, протянулась бы на несколько километров. Однако любая математическая теория вынуждена начинаться с некоторых неопределяемых понятий и аксиом или постулатов относительно них. Так как положительные целые числа хорошо известны и трудно определить их с помощью чего-то более простого, мы примем их за исходные неопределяемые понятия и будем считать, что основные свойства этих чисел известны.
Отрицательные целые числа и нуль.
Отрицательные числа в наши дни вещь обыденная: их используют, например, для того, чтобы представить температуру ниже нуля. Поэтому кажется удивительным, что еще несколько столетий назад какой-либо конкретной интерпретации отрицательных чисел не было, а возникающие по ходу вычислений отрицательные числа назывались «воображаемыми». Несмотря на то, что интуитивная интерпретация отрицательных чисел сама по себе полезна, пытаясь понять такие «правила», как (–4)ґ(–3) = +12, мы должны определить отрицательные числа с помощью положительных. Для этого нам нужно построить множество таких математических объектов, которые будут вести себя в арифметике и алгебре именно так, как можно было бы ожидать от отрицательных чисел. Один из способов построить такое множество состоит в рассмотрении упорядоченных пар положительных чисел (a,b). «Упорядоченность» означает, что, например, пара (2,3) отлична от пары (3,2). Такие упорядоченные пары можно рассматривать как новый класс чисел. Теперь мы должны сказать, когда два таких новых числа равны и что означает их сложение и умножение. Наш выбор определений обусловлен желанием, чтобы пара (a,b) действовала как разность (a – b), которая пока что определена, лишь когда a больше b. Так как в алгебре (a – b) + (c – d) = (a + c) – (b + d), мы приходим к необходимости определить сложение новых чисел как (a,b) + (c,d) = (a + c, b + d); т.к. (a – b)ґ(c – d) = ac + bd – (bc + ad), мы определяем умножение равенством (a,b)ґ(c,d) = (ac + bd, bc + ad); а так как (a – b) = (c – d), если a + d = b + c, мы определяем равенство новых чисел соотношением (a,b) = (c,d), если a + d = b + c. Таким образом,
Используя определения равенства пар, можно записать сумму и произведение пар в более простом виде:
Все пары (a,a) равны (по определению равенства пар) и действуют так, как по нашим ожиданиям должен действовать нуль. Например, (2,3) + (1,1) = (3,4) = (2,3); (2,3)ґ(1,1) = (2 + 3, 2 + 3) = (5,5) = (1,1). Пары (a,a) мы можем обозначить символом 0 (который до сих пор не использовали).
Пары (a,b), где b больше a, ведут себя так, как должны были бы действовать отрицательные числа, и мы можем обозначить пару (a,b) символом –(b – a). Например, -4 – это (1,5), а -3 – это (1,4); (–4)ґ(–3) = (21,9), или (13,1). Последнее число хотелось бы обозначить как 12, но это заведомо не то же самое, что положительное целое число 12, поскольку обозначает пару положительных целых чисел, а не одно положительное целое число. Необходимо подчеркнуть, что поскольку пары (a,b), где b меньше a, действуют как положительные целые числа (a – b), мы будем записывать такие числа как (a – b). При этом надо забыть о положительных целых числах, с которых мы начали, и впредь пользоваться только нашими новыми числами, которые назовем целыми числами. То, что мы намереваемся использовать старые названия для некоторых новых чисел, не должно вводить в заблуждение относительно того, что в действительности новые числа представляют собой объекты иного рода.
Дроби.
Интуитивно мы представляем себе дробь 2/3 как результат разбиения 1 на три равные части и взятия двух из них. Однако математик стремится как можно меньше полагаться на интуицию и определять рациональные числа через более простые объекты – целые числа. Это можно сделать, если 2/3 рассматривать как упорядоченную пару (2,3) целых чисел. Для завершения определения необходимо сформулировать правила равенства дробей, а также сложения и умножения. Разумеется, эти правила должны быть эквивалентны правилам арифметики и, естественно, отличаться от правил для тех упорядоченных пар, которые мы определили как целые числа. Вот эти правила:
Нетрудно видеть, что пары (a,1) действуют как целые числа a; продолжая рассуждать так же, как в случае отрицательных чисел, мы обозначим через 2 дробь (2,1), или (4,2), или любую другую дробь, равную (2,1). Забудем теперь о целых числах и сохраним их лишь как средство записи определенных дробей.
Рациональные и иррациональные числа.
Дроби принято также называть рациональными числами, так как они представимы в виде отношений (от лат. ratio – отношение) двух целых чисел. Но если нам потребуется число, квадрат которого равен 2, то мы не сможем обойтись рациональными числами, т.к. не существует рационального числа, квадрат которого равен 2. То же самое выяснится, если поинтересоваться числом, выражающим отношение длины окружности к ее диаметру. Следовательно, если мы хотим получить квадратные корни из всех положительных чисел, то нам необходимо расширить класс рациональных чисел. Новые числа, называемые иррациональными (т.е. не рациональными), можно определять различными способами. Упорядоченные пары для этого не годятся; один из простейших способов состоит в том, чтобы определить иррациональные числа как бесконечные непериодические десятичные дроби.
Действительные числа.
Рациональные и иррациональные числа вместе называются действительными или вещественными числами. Геометрически их можно представить точками на прямой, при этом дроби оказываются в промежутках между целыми числами, а иррациональные числа – в промежутках между дробями, как показано на рис. 1. Можно показать, что система действительных чисел обладает свойством, известным как «полнота» и означающим, что каждой точке на прямой соответствует некоторое действительное число.
Комплéксные числа.
Так как квадраты положительных и отрицательных действительных чисел положительны, на прямой действительных чисел нет точки, соответствующей числу, квадрат которого был бы равен -1. Но если бы мы попытались решать квадратные уравнения типа x2 + 1 = 0, то необходимо было бы поступать так, как если бы существовало некоторое число i, квадрат которого был бы равен -1. Но поскольку такого числа нет, нам не остается ничего другого, как воспользоваться «воображаемым», или «мнимым», числом. Соответственно, «число» i и его комбинации с обычными числами (типа 2 + 3i) стали называться мнимыми. Современные математики предпочитают называть такие числа «комплéксными», поскольку они, как мы увидим, столь же «реальны», как и те, с которыми нам уже доводилось встречаться раньше. Долгое время математики свободно пользовались мнимыми числами и получали полезные результаты, хотя не до конца понимали то, что они делали. И до начала 19 в. никому и в голову не приходило «оживить» мнимые числа с помощью их явного определения. Для этого нужно построить некоторую совокупность математических объектов, которые с точки зрения алгебры вели бы себя как выражения a + bi, если условиться, что i 2 = –1. Такие объекты можно определить следующим образом. Рассмотрим в качестве наших новых чисел упорядоченные пары действительных чисел, сложение и умножение которых определяется формулами:
Например,
Назовем такие упорядоченные пары комплéксными числами. Пары частного вида (a,0) со вторым членом, равным нулю, ведут себя как действительные числа, поэтому мы условимся обозначать их так же: например, 2 означает (2,0). С другой стороны, комплексное число (0,b) по определению умножения обладает свойством (0,b)ґ(0,b) = (0 – b2, 0 + 0) = (–b2,0) = –b2. Например, в случае (0,1)ґ(0,1) мы находим произведение (-1,0); следовательно, (0,1)2 = (–1,0). Мы уже условились записывать комплексное число (-1,0) как -1, поэтому если число (0,1) обозначить символом i, то мы получим комплексное число i, такое, что i 2 = –1. Кроме того, комплексное число (2,3) теперь можно записать в виде 2 + 3i.
Важное отличие такого подхода к комплексным числам от традиционного состоит в том, что в данном случае число i не содержит ничего загадочного или мнимого: оно представляет собой нечто, хорошо определяемое посредством уже существовавших ранее чисел, хотя, разумеется, и не совпадает ни с одним из них. Точно так же, действительное число 2 не является комплексным, хотя мы и используем символ 2 для обозначения комплексного числа. Так как на самом деле в мнимых числах нет ничего «мнимого», то неудивительно, что они широко используются в реальных ситуациях, например в электротехнике (где вместо буквы i обычно используют букву j, так как в электротехнике i – символ для текущего значения силы тока).
Алгебра комплексных чисел во многом напоминает алгебру действительных чисел, хотя имеются и существенные различия. Например, правило 
для комплексных чисел не выполняется: 
, поэтому 
, в то время как 
.
Определение комплексных чисел как пар действительных чисел подсказывает способ их наглядного геометрического представления. Хотя прямая не может вместить и действительные, и комплексные числа, их вполне может вместить плоскость (см. рис. 2,а). Например, число 2 + 3i представлено точкой плоскости с координатами (2,3) (см. также АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ).
Сложение комплексных чисел допускает простую геометрическую интерпретацию. Например, сумма чисел 2 + 3i и 3 – i есть число 5 + 2i, которому соответствует четвертая вершина параллелограмма с тремя вершинами в точках 0, 2 + 3i и 3 – i.
Точку на плоскости можно задавать не только прямоугольными (декартовыми) координатами (x,y), но и ее полярными координатами (r,q), задающими расстояние от точки до начала координат и угол. Следовательно, комплексное число x + iy может быть записано и в полярных координатах (рис. 2,б). Длина радиуса-вектора r равна расстоянию от начала координат до точки, соответствующей комплексному числу; величина r называется модулем комплексного числа и определяется по формуле 
. Часто модуль записывают в виде 
. Угол q называется «углом», «аргументом» или «фазой» комплексного числа. Такое число имеет бесконечно много углов, отличающихся на величину, кратную 360°; например, i имеет угол 90°, 450°, -270°, ј Так как декартовы и полярные координаты одной и той же точки связаны между собой соотношениями x = r cos q, y = r sin q, справедливо равенство x + iy = r (cos q + i sin q).
Если z = x + iy, то число x – iy называется комплексно сопряженным с z и обозначается 
, а в технике z*. Формула 
= r2 удобна для вычисления модуля комплексного числа z, особенно если это число определяется сложной формулой.
Пользуясь формулами тригонометрии, находим:
Отсюда правило: чтобы перемножить два комплексных числа, необходимо умножить их модули и сложить их аргументы. В частности, квадрат числа r (cos q + i sin q) равен r2(cos 2q + i sin 2q), более общая, n-я степень того же числа равна r n(cos nq + i sin nq) (формула Муавра). Эта формула справедлива при надлежащей интерпретации, даже если n – не положительное целое число. Например,
Следовательно, можно ожидать, что кубический корень из 8i (n = 1/3) будет равен
Поскольку аргумент числа i можно считать равным и 90° + 360° = 450°, и 90° + 360° + 360° = 810°, мы можем найти еще два кубических корня из 8i, а именно:
и
(рис. 3). Любое комплексное число (кроме нуля) также имеет три кубических корня (геометрически расположенных в вершинах равностороннего треугольника) и n корней n-й степени, если n – положительное целое число.
Так как мы можем определить целые степени и корни из комплексных чисел, можно ввести и любую рациональную степень, например (2 + i)–3/4. Сложнее определить иррациональные или комплексные степени. Прежде всего необходимо ввести экспоненциальную функцию. Это можно сделать, используя ее разложение в степенной ряд
Известно, что если q – действительное число, то eiq определяется этим степенным рядом и eiq = cos q + i sin q; следовательно, тригонометрическая форма комплексного числа представима в компактном виде z = reiq. Логарифм комплексного числа reiq, по определению, равен ln r + iq, где ln означает логарифм по основанию e, а q принимает все возможные значения, измеряемые в радианах. Таким образом, комплексное число имеет бесконечно много логарифмов. Например, ln (–2) = ln 2 + ip + любое целое кратное 2p. В общем виде степени можно теперь определить с помощью соотношения ab = e b ln a. Например, i–2i = e –2 ln i. Так как значения аргумента числа i равны p/2 (90°, выраженное в радианах) плюс целое кратное, то число i–2i имеет значения ep, e3p, e-p и т.д., которые все являются действительными.
Гиперкомплексные числа.
Комплексные числа были изобретены, чтобы иметь возможность решать все квадратные уравнения с действительными коэффициентами. Можно показать, что на самом деле комплексные числа позволяют сделать гораздо больше: с их введением становятся разрешимыми алгебраические уравнения любой степени даже с комплексными коэффициентами. Следовательно, если бы нас интересовали только решения алгебраических уравнений, то необходимость во введении новых чисел отпала бы. Однако для других целей необходимы числа, устроенные в чем-то аналогично комплексным, но с бóльшим количеством компонент. Иногда такие числа называют гиперкомплексными. Их примерами могут служить кватернионы и матрицы.
Ответь на вопросы викторины «Математика»