АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Содержание статьи

• Прямые.
• Парабола.
• Преобразование уравнений.
• АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
• Более высокие размерности.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ, раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р.Декарту, изложившему ее основы в последней главе своего трактата Рассуждение о методе, озаглавленной Геометрия (1637). Однако сам метод был известен П.Ферма еще в 1629, о чем свидетельствует его переписка. Аналитическая геометрия стала неоценимым подспорьем для математического анализа, изобретенного вскоре Ньютоном (1665–1666) и Лейбницем (1675–1676).

Методы аналитической геометрии применимы к фигурам на плоскости и к поверхностям в трехмерном пространстве, а также допускают естественное обобщение и на пространства более высоких размерностей. Мы начнем с аналитической геометрии на плоскости.

Сущность метода координат состоит в следующем. На плоскости задаются две взаимно перпендикулярные прямые (координатные оси), пересекающиеся в точке О, называемой началом координат. Одна из них – ось x, или ось абсцисс, обычно выбирается горизонтальной, другая – ось y, или ось ординат, – вертикальной. Справа от O выбирается точка, у которой ставится отметка 1. Если принять отрезок от O до 1 за единицу длины, то откладывая последовательно этот отрезок вдоль прямой, мы получаем числовую ось. Считается, что эта ось продолжается вправо до бесконечности. Точки на оси x слева от O помечаются отрицательными числами, как на шкале термометра. Например, точка -2 расположена от точки O слева на таком же расстоянии, как точка 2 справа. Аналогичным образом с той же единицей длины размечается и ось y. Положительные числа располагаются выше точки O, отрицательные – ниже.

Пусть P – любая точка на плоскости с заданной системой координат, Q – основание перпендикуляра, опущенного из P на ось x, а R – основание перпендикуляра, опущенного из P на ось y. Положение точки P полностью определяется двумя числами, называемыми координатами x и y. Первая координата указывает положение точки Q на оси x, вторая – положение точки R на оси y. На рис. 1 положение точки P полностью определяется ее координатами (2,3).

Основная задача аналитической геометрии заключается в изучении геометрических фигур с помощью соотношений между координатами точек, из которых эти фигуры образованы. Любую фигуру можно рассматривать как множество точек, удовлетворяющих некоторому геометрическому условию. Это условие можно записать в виде алгебраического уравнения, связывающего координаты x и y каждой точки фигуры. Суть метода аналитической геометрии состоит в изучении свойств фигуры с помощью соответствующего уравнения, исследуемого средствами алгебры. Этот метод позволяет устанавливать геометрические факты систематичным образом, в отличие от традиционной «синтетической» геометрии, где приходилось изобретать методы доказательства для каждого отдельного случая.

Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точками P₁ = (x₁,y₁) и P₂ = (x₂,y₂). Числа x₁, y₁, x₂ и y₂ могут быть любыми действительными числами, положительными, отрицательными или 0. На рис. 2 все числа выбраны положительными. Проведем через точку P₁ горизонтальную прямую, а через точку P₂ – вертикальную. Пусть R – точка их пересечения. Тогда по теореме Пифагора

откуда

d ² = (x₂ – x₁)² + (y₂ – y₁)².

Это и есть формула для вычисления расстояния между двумя точками.

Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки P₁ и P₂. Например, если точка P₂ расположена ниже точки P₁ и справа от нее, как на рис. 3, то отрезок RP₂ можно считать равным y₁ – y₂, а не y₂ – y₁. Расстояние между точками, вычисляемое по формуле, от этого не изменится, так как (y₁ – y₂)² = (y₂ – y₁)². Заметим, что так как величина y₂ в этом случае отрицательна, разность y₁ – y₂ больше, чем y₁, как и должно быть.

Прямые.

Прямая – одна из простейших геометрических фигур. Алгебраическое уравнение прямой также имеет простой вид.

Пусть B = (0,b)– точка пересечения прямой L с осью y, а P = (x,y) – любая другая точка на этой прямой. Проведем через точку B прямую, параллельную оси x, а через точку P – прямую, параллельную оси y; проведем также прямую x = 1. Пусть m – угловой коэффициент прямой L (см. рис. 4). Так как треугольники BSQ и BRP подобны, то

или, после упрощения,

Следовательно, если точка P лежит на прямой L, то ее координаты удовлетворяют уравнению (1). Обратно, нетрудно показать, что если x и y связаны между собой уравнением (1), то точка P непременно лежит на прямой L, проходящей через точку (0,b) и имеющей угловой коэффициент m.

Таким образом, уравнение любой прямой можно записать в виде

В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени по x и y можно привести к виду (2) либо (3).

Рассмотрим произвольное уравнение первой степени

Если B № 0, мы можем записать уравнение (4) в виде

т.е. в виде (2). При B = 0 уравнение (4) сводится к уравнению

Ax = C,

или

т.е. к уравнению вида (3).

Таким образом, любая прямая описывается уравнением первой степени по x и y, и обратно, каждое уравнение первой степени по x и y соответствует некоторой прямой.

Парабола.

Методы аналитической геометрии позволяют без особых трудностей исследовать свойства кривых, которые обычно не рассматриваются в стандартных учебниках планиметрии.

Пусть заданы точка F с координатами (0,1) и прямая y = –1 (рис. 5). Множество точек P = (x,y), для которых расстояние PF равно расстоянию PD, называется параболой. Прямая y = –1 называется директрисой параболы, а точка F – фокусом параболы. Чтобы выяснить, как располагаются точки P, удовлетворяющие условию PF = PD, запишем его с помощью координат:

x² + (y – 1)² = (y + 1)² + (x – x)²,

или после упрощения x² = 4y. Это уравнение геометрического места точек, образующих параболу.

Рассмотрим теперь точки пересечения произвольной невертикальной прямой y = mx + b с параболой x² = 4y. Точки пересечения должны иметь координаты, удовлетворяющие одновременно обоим уравнениям, поэтому

x² = 4mx + 4b,

или

x² – 4mx – 4b = 0.

В общем случае существуют два решения x₁ и x₂ квадратного уравнения. Известно, что сумма этих решений x₁ + x₂ равна коэффициенту при x, взятому со знаком минус. Следовательно,

x₁ + x₂ = 4m.

Абсцисса средней точки M хорды P₁P₂ равна

Результат зависит только от m и не зависит от b.

Если теперь мы рассмотрим множество параллельных прямых с одним и тем же угловым коэффициентом m, но с различными значениями b, то середины всех хорд, высекаемых на этих прямых параболой, лежат на вертикальной прямой x = 2m (см. рис. 6).

Среди этих параллельных прямых есть одна особенная прямая T, пересекающая параболу только в одной точке. Эта прямая называется касательной. Точка касания P имеет координаты (2m,m²).

Преобразование уравнений.

Уравнение кривой зависит от положения координатных осей и от выбранных масштабов. Например, уравнение окружности с радиусом r единиц и с центром в начале координат имеет вид

x² + y² = r².

Но если окружность расположена так, как показано на рис. 7, с центром в точке с координатами (h,k), то ее уравнение принимает более сложный вид:

(x – h)² + (y – k)² = r²,

в чем нетрудно убедиться, воспользовавшись формулой расстояния. Для исследования свойств кривой удобно расположить оси так, чтобы уравнение приняло по возможности более простой вид, как мы поступили в случае параболы.

До сих пор мы исследовали кривую, заданную некоторым геометрическим условием, которому должны удовлетворять все принадлежащие ей точки, и вывели уравнение относительно заданной пары координатных осей. Обратная задача состоит в том, чтобы построить кривую, соответствующую данному уравнению, и исследовать геометрические свойства этой кривой или ее графика.

Предположим, что мы хотим исследовать график кривой

Перепишем это соотношение в виде

y = x² – 2x + 1 + 2 = (x – 1)² + 2.

Сделав затем замену переменных xў = x – 1 è yў = y – 2, сведем (5) к следующему уравнению:

которое, конечно, гораздо проще. Теперь заданную кривую можно записать в новой системе, оси которой параллельны старым с началом координат в точке x = 1, y = 2. Помимо такого приема (называемого параллельным переносом) – сдвига осей координат по горизонтали и по вертикали на соответствующие величины, уравнения часто упрощаются после поворота системы координат на некоторый угол вокруг неподвижного начала координат O.

Оказывается, что этих двух приемов – параллельного переноса и поворота координатных осей, выполняемых по отдельности или вместе, – вполне достаточно, чтобы привести уравнение второй степени или к уравнениям двух прямых (пересекающихся, параллельных или совпадающих) или к одному из стандартных видов:

Уравнение (7) описывает параболу с фокусом в точке (0,p) и директрисой y = – p. Уравнение (8) соответствует эллипсу. Уравнение (9) описывает гиперболу (см. также КОНИЧЕСКИЕ СЕЧЕНИЯ).

Помимо исследования графиков алгебраических уравнений, аналитическая геометрия изучает также неалгебраические, или трансцендентные, кривые, например графики экспоненциальных, логарифмических и тригонометрических функций. В качестве примера трансцендентной кривой приведем циклоиду – кривую, описываемую точкой окружности, катящейся без скольжения по прямой (рис. 8). Если в качестве прямой выбрать ось абсцисс, а радиус окружности принять равным 1, то координаты точки P будут иметь вид

где q – угол в радианах.

Циклоида обладает многими замечательными свойствами. Длина дуги циклоиды в 8 раз больше, чем длина катящейся окружности, а площадь под дугой в 3 раза больше площади катящегося круга. Если циклоиду перевернуть, то мы получим форму нити, по которой бусина соскальзывала бы до данной точки за кратчайшее время. Эти результаты доказываются методами математического анализа, а последний из них – методами вариационного исчисления. Циклоиды и аналогичные кривые, возникающие при движении одной окружности по другой, играют важную роль при проектировании зубчатых передач, действующих бесшумно и эффективно. На рис. 9 вы видите несколько других кривых и их уравнения.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

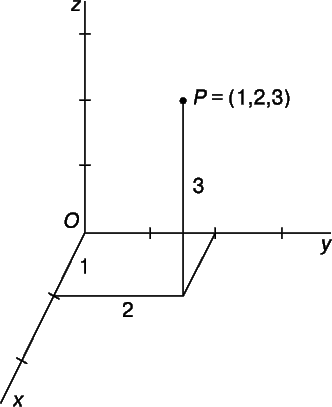
Методами аналитической геометрии исследуются также и пространственные фигуры. Нужно лишь воспользоваться тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось шкалой, можно задать тремя числами (координатами) положение точки в пространстве. Например (рис. 10), P = (1,2,3).

Множеству точек, удовлетворяющих некоторому геометрическому условию, соответствует определенное алгебраическое соотношение между их координатами x, y, z. Для задания этого соответствия необходима фундаментальная формула, определяющая расстояние d между точками P₁ = (x₁, y₁, z₁) и P₂ = (x₂, y₂, z₂), а именно:

d² = (x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)².

Эта формула представляет собой обобщение теоремы Пифагора с двумерного случая на трехмерный. Из нее следует, что сфера радиуса r с центром в начале координат описывается уравнением

x² + y² + z² = r².

Любая плоскость задается уравнением первой степени относительно x, y и z, т.е. уравнением вида

Ax + By + Cz = D,

где A, B, C и D – постоянные и, по крайней мере, один из коэффициентов A, B или C не равен нулю. Помимо сферы есть и другие поверхности, также описываемые уравнением второй степени относительно x, y и z. Одна из задач аналитической геометрии в трехмерном пространстве состоит в том, чтобы дать классификацию таких квадратичных поверхностей и, исходя из соответствующих им уравнений, исследовать их свойства. Эти поверхности называются эллипсоидами, параболоидами, гиперболоидами или коническими и цилиндрическими поверхностями различных типов. Особенно простой подкласс этих фигур состоит из поверхностей, получаемых при вращении конических сечений вокруг различных осей симметрии.

Существуют многочисленные поверхности, задаваемые уравнениями более высокого порядка. Как правило, они довольно сложны. Их изучением, как и плоских кривых высокого порядка, занимается алгебраическая геометрия.

Как и в случае фигур на плоскости, исследование трехмерных геометрических тел часто облегчается подходящим выбором координатных осей. Соответствующее уравнение обычно удается упростить с помощью параллельного переноса и (или) поворота осей. Иногда бывает удобно воспользоваться непрямоугольной системой координат. Например, если в уравнение, записанное в прямоугольных координатах x, y и z, подставить x = r cos q, y = r sin q и z = z, то получится эквивалентное и нередко более простое уравнение в цилиндрических координатах r, q и z (рис. 11). Так, уравнение z = x² + y² сводится к уравнению z = r².

Подстановка

x = r cos q sin f, y = r sin q sin f, z = r cos f

преобразует уравнение, заданное в прямоугольных координатах, в уравнение в сферических координатах r, q и f (рис. 12).

Аналитическая геометрия занимается также изучением прямых и кривых в трехмерном пространстве. Прямую можно рассматривать как линию пересечения подходящей пары плоскостей. Соответственно, пространственную прямую можно задать с помощью двух уравнений первого порядка. Однако часто бывает проще задать прямую L с помощью параметра t следующим образом:

x = x₀ + a₁t, y = y₀ + a₂t, z = z₀ + a₃t.

Когда t принимает все возможные действительные значения, мы получаем все возможные значения x, y и z для точек на L. При t = 0 мы получаем координаты x₀, y₀ и z₀ некоторой точки P₀; при t = 1 – координаты (x₀ + a₁, y₀ + a₂, z₀ + a₃) некоторой другой точки P₁. Прямая L определяется двумя своими точками P₀ и P₁.

Пространственную кривую можно также записать в виде

x = f₁(t), y = f₂(t), z = f₃(t),

где f₁, f₂ и f₃ – заданные функции. (Прямая соответствует случаю, когда все три функции имеют первую степень по t.)

Например,

x = cos t, y = sin t, z = t

– уравнения винтовой линии, получающейся при наматывании нити на цилиндрическую поверхность радиуса 1 с постоянным шагом (рис. 13).

Более высокие размерности.

Вполне естественно обобщить методы аналитической геометрии на случаи, когда число координат больше трех. Разумеется, невозможно представить себе наглядно гиперсферу x² + y² + z² + w² = r² или гиперплоскость Ax + By + Cz + Dw = E. И все же мы можем воспользоваться теми же алгебраическими методами, как и в случаях двух или трех измерений, используя соответствующий им наглядный геометрический язык как подсказку, когда такая наглядность отсутствует. Более того, весьма плодотворным оказалось обобщение методов аналитической геометрии на бесконечномерные пространства.

Многие важные разделы аналитической геометрии пространства трех и более измерений можно существенно упростить с помощью векторных методов (см. также ВЕКТОР).