ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ, раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях.
ЭЛЕКТРОСТАТИКА
В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между такими зарядами, было отмечено еще во времена Гомера. Слово «электричество» происходит от греческого °lektron (янтарь), поскольку первые описанные в истории наблюдения электризации трением связаны именно с этим материалом. В 1733 Ш.Дюфе (1698–1739) открыл, что существуют электрические заряды двух типов. Заряды одного типа образуются на сургуче, если его натирать шерстяной тканью, заряды другого типа – на стекле, если его натирать шелком. Одинаковые заряды отталкиваются, разные – притягиваются. Заряды разных типов, соединяясь, нейтрализуют друг друга. В 1750 Б.Франклин (1706–1790) разработал теорию электрических явлений, основанную на предположении, что все материалы содержат некую «электрическую жидкость». Он полагал, что при трении двух материалов друг о друга часть этой электрической жидкости переходит с одного из них на другой (при этом общее количество электрической жидкости сохраняется). Избыток электрической жидкости в теле сообщает ему заряд одного типа, а ее недостаток проявляется как наличие заряда другого типа. Франклин решил, что при натирании сургуча шерстяной тканью шерсть отнимает у него некоторое количество электрической жидкости. Поэтому он назвал заряд сургуча отрицательным.
Взгляды Франклина очень близки современным представлениям, согласно которым электризация трением объясняется перетеканием электронов с одного из трущихся тел на другое. Но поскольку в действительности электроны перетекают с шерсти на сургуч, в сургуче возникает избыток, а не недостаток этой электрической жидкости, которая теперь отождествляется с электронами. У Франклина не было способа определить, в каком направлении перетекает электрическая жидкость, и его неудачному выбору мы обязаны тем, что заряды электронов оказались «отрицательными». Хотя такой знак заряда вызывает некоторую путаницу у приступающих к изучению предмета, эта условность слишком прочно укоренилась в литературе, чтобы говорить об изменении знака заряда у электрона после того, как его свойства уже хорошо изучены.
С помощью крутильных весов, разработанных Г.Кавендишем (1731–1810), в 1785 Ш.Кулон (1736–1806) показал, что сила, действующая между двумя точечными электрическими зарядами, пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния между ними, а именно:

где F – сила, с которой заряд q отталкивает заряд того же знака qў, а r – расстояние между ними. Если знаки зарядов противоположны, то сила F отрицательна и заряды не отталкивают, а притягивают друг друга. Коэффициент пропорциональности K зависит от того, в каких единицах измеряются F, r, q и qў.
Единицы измерения заряда первоначально не существовало, но закон Кулона дает возможность ввести такую единицу. Этой единице измерения электрического заряда присвоено название «кулон» и сокращенное обозначение Кл. Один кулон (1 Кл) представляет собой заряд, который остается на первоначально электрически нейтральном теле после удаления с него 6,242Ч1018 электронов.
Если в формуле (1) заряды q и qў выражены в кулонах, F – в ньютонах, а r – в метрах, то K » 8,9876Ч109 HЧм2/Кл2, т.е. примерно 9Ч109 НЧм2/Кл2. Обычно вместо K используют константу e0 = 1/4pK. Хотя при этом выражение для закона Кулона немного усложняется, это позволяет обходиться без множителя 4p в других формулах, которые применяются чаще закона Кулона.
Электростатические машины и лейденская банка.
Машину для получения статического заряда большой величины путем трения изобрел примерно в 1660 О.Герике (1602–1686), описавший ее в книге Новые опыты о пустом пространстве (De vacuo spatio, 1672). Вскоре появились другие варианты такой машины. В 1745 Э.Клейст из Каммина и независимо от него П.Мушенбрук из Лейдена обнаружили, что стеклянную посудину, выложенную изнутри и снаружи проводящим материалом, можно использовать для накопления и хранения электрического заряда. Стеклянные банки, выложенные изнутри и снаружи оловянной фольгой – так называемые лейденские банки – были первыми электрическими конденсаторами. Франклин показал, что при зарядке лейденской банки наружное покрытие из оловянной фольги (наружная обкладка) приобретает заряд одного знака, а внутренняя обкладка – равный по величине заряд противоположного знака. Если обе заряженные обкладки приводятся в соприкосновение или соединяются проводником, то заряды полностью исчезают, что свидетельствует об их взаимной нейтрализации. Отсюда следует, что заряды свободно перемещаются по металлу, но не могут перемещаться по стеклу. Материалы типа металлов, по которым заряды передвигаются свободно, были названы проводниками, а материалы типа стекла, через которые заряды не проходят, – изоляторами (диэлектриками).
Диэлектрики.
Идеальный диэлектрик – это материал, внутренние электрические заряды которого связаны настолько прочно, что он не способен проводить электрический ток. Поэтому он может служить хорошим изолятором. Хотя идеальных диэлектриков в природе не существует, проводимость многих изоляционных материалов при комнатной температуре не превышает 10–23 проводимости меди; во многих случаях такую проводимость можно считать равной нулю.
Проводники.
Кристаллическая структура и распределение электронов в твердых проводниках и диэлектриках сходны между собой. Основное различие заключается в том, что в диэлектрике все электроны прочно связаны с соответствующими ядрами, тогда как в проводнике имеются электроны, находящиеся во внешней оболочке атомов, которые могут свободно перемещаться по кристаллу. Такие электроны называют свободными электронами или электронами проводимости, поскольку они являются переносчиками электрического заряда. Число электронов проводимости, приходящихся на один атом металла, зависит от электронной структуры атомов и степени возмущения внешних электронных оболочек атома его соседями по кристаллической решетке. У элементов первой группы периодической системы элементов (лития, натрия, калия, меди, рубидия, серебра, цезия и золота) внутренние электронные оболочки заполнены целиком, а во внешней оболочке имеется один-единственный электрон. Эксперимент подтвердил, что у этих металлов приходящееся на один атом число электронов проводимости приблизительно равно единице. Однако для большинства металлов других групп характерны в среднем дробные значения числа электронов проводимости в расчете на один атом. Например, у переходных элементов – никеля, кобальта, палладия, рения и большинства их сплавов – число электронов проводимости на один атом равно примерно 0,6. Число носителей тока в полупроводниках гораздо меньше. Например, в германии при комнатной температуре оно порядка 10–9. Чрезвычайно малое число носителей в полупроводниках приводит к возникновению у них множества интересных свойств.
См. ФИЗИКА ТВЕРДОГО ТЕЛА; ПОЛУПРОВОДНИКОВЫЕ ЭЛЕКТРОННЫЕ ПРИБОРЫ; ТРАНЗИСТОР.
Тепловые колебания кристаллической решетки в металле поддерживают постоянное движение электронов проводимости, скорость которых при комнатной температуре достигает 106 м/с. Поскольку это движение хаотично, оно не приводит к возникновению электрического тока. При наложении же электрического поля появляется небольшой общий дрейф. Этот дрейф свободных электронов в проводнике и представляет собой электрический ток. Поскольку электроны заряжены отрицательно, направление тока противоположно направлению их дрейфа.
Разность потенциалов.
Для описания свойств конденсатора необходимо ввести понятие разности потенциалов. Если на одной обкладке конденсатора имеется положительный заряд, а на другой – отрицательный заряд той же величины, то для переноса дополнительной порции положительного заряда с отрицательной обкладки на положительную необходимо совершить работу против сил притяжения со стороны отрицательных зарядов и отталкивания положительных. Разность потенциалов между обкладками определяется как отношение работы по переносу пробного заряда к величине этого заряда; при этом предполагается, что пробный заряд значительно меньше заряда, находившегося первоначально на каждой из обкладок. Несколько видоизменив формулировку, можно дать определение разности потенциалов между любыми двумя точками, которые могут находиться где угодно: на проводе с током, на разных обкладках конденсатора либо просто в пространстве. Это определение таково: разность потенциалов между двумя точками пространства равна отношению работы, затрачиваемой на перемещение пробного заряда из точки с более низким потенциалом в точку с более высоким потенциалом, к величине пробного заряда. Снова предполагается, что пробный заряд достаточно мал и не нарушает распределения зарядов, создающих измеряемую разность потенциалов. Разность потенциалов V измеряется в вольтах (В) при условии, что работа W выражена в джоулях (Дж), а пробный заряд q – в кулонах (Кл).
Емкость.
Емкость конденсатора равна отношению абсолютной величины заряда на любой из двух его обкладок (напомним, что их заряды различаются только знаком) к разности потенциалов между обкладками:

Емкость C измеряется в фарадах (Ф), если заряд Q выражен в кулонах (Кл), а разность потенциалов – в вольтах (В). Две только что упомянутые единицы измерения, вольт и фарада, названы так в честь ученых А.Вольты и М.Фарадея.
Фарада оказалась настолько крупной единицей, что емкость большинства конденсаторов выражают в микрофарадах (10–6 Ф) или пикофарадах (10–12 Ф).
Электрическое поле.
Вблизи электрических зарядов существует электрическое поле, величина которого в данной точке пространства равна, по определению, отношению силы, действующей на точечный пробный заряд, помещенный в эту точку, к величине пробного заряда, опять-таки при условии, что пробный заряд достаточно мал и не изменяет распределения зарядов, создающих поле. Согласно этому определению, действующая на заряд q сила F и напряженность электрического поля E связаны соотношением

Фарадей ввел представление о силовых линиях электрического поля, начинающихся на положительных и оканчивающихся на отрицательных зарядах. При этом плотность (густота) силовых линий пропорциональна напряженности поля, а направление поля в данной точке совпадает с направлением касательной к силовой линии. Позднее К.Гаусс (1777–1855) подтвердил справедливость этой догадки. Исходя из установленного Кулоном закона обратных квадратов (1), он математически строго показал, что силовые линии, если их строить в соответствии с представлениями Фарадея, непрерывны повсюду в пустом пространстве, начинаясь на положительных зарядах и заканчиваясь на отрицательных. Это обобщение получило наименование теоремы Гаусса. Если полное число силовых линий, выходящих из каждого заряда Q, равно Q/e0, то плотность линий в любой точке (т.е. отношение числа линий, пересекающих воображаемую площадку малого размера, помещенную в эту точку перпендикулярно им, к площади этой площадки) равна величине напряженности электрического поля в этой точке, выраженной либо в Н/Кл, либо в В/м.
Простейший конденсатор представляет собой две параллельные проводящие пластины, расположенные близко друг к другу. При зарядке конденсатора пластины приобретают одинаковые, но противоположные по знаку заряды, равномерно распределенные по каждой из пластин, за исключением краев. Согласно теореме Гаусса, напряженность поля между такими пластинами постоянна и равна E = Q/e0A, где Q – заряд на положительно заряженной пластине, а А – площадь пластины. В силу определения разности потенциалов имеем  , где d – расстояние между пластинами. Таким образом, V = Qd/e0A, и емкость такого плоскопараллельного конденсатора равна:
, где d – расстояние между пластинами. Таким образом, V = Qd/e0A, и емкость такого плоскопараллельного конденсатора равна:

где C выражается в фарадах, а A и d, соответственно, в м2 и м.
ПОСТОЯННЫЙ ТОК
В 1780 Л.Гальвани (1737–1798) заметил, что заряд, подводимый от электростатической машины к лапке мертвой лягушки, заставляет лапку резко дергаться. Более того, лапки лягушки, закрепленной над железной пластинкой на латунной проволочке, введенной в ее спинной мозг, дергались всякий раз, как только касались пластинки. Гальвани правильно объяснил это тем, что электрические заряды, проходя по нервным волокнам, заставляют мышцы лягушки сокращаться. Это движение зарядов было названо гальваническим током.
После опытов, проводившихся Гальвани, Вольта (1745–1827) изобрел так называемый вольтов столб – гальваническую батарею из нескольких последовательно соединенных электрохимических элементов. Его батарея состояла из чередовавшихся медных и цинковых кружочков, разделенных влажной бумагой, и позволяла наблюдать те же явления, что и электростатическая машина.
Повторяя опыты Вольты, Никольсон и Карлейль в 1800 обнаружили, что посредством электрического тока можно нанести медь из раствора сульфата меди на медный проводник. У.Волластон (1766–1828) получил такие же результаты с помощью электростатической машины. М.Фарадей (1791–1867) показал в 1833, что масса элемента, получаемого с помощью электролиза, производимого данным количеством заряда, пропорциональна его атомной массе, деленной на валентность. Это положение ныне называют законом Фарадея для электролиза.
Поскольку электрический ток представляет собой перенос электрических зарядов, естественно определить единицу силы тока как заряд в кулонах, который ежесекундно проходит через данную площадку. Сила тока 1 Кл/с была названа ампером в честь А.Ампера (1775–1836), открывшего многие важные эффекты, связанные с действием электрического тока.
Закон Ома, сопротивление и удельное сопротивление.
В 1826 Г.Ом (1787–1854) сообщил о новом открытии: ток в металлическом проводнике при введении в цепь каждой дополнительной секции вольтова столба возрастал на одну и ту же величину. Это было обобщено в виде закона Ома. Поскольку создаваемая вольтовым столбом разность потенциалов пропорциональна числу включенных секций, этот закон утверждает, что разность потенциалов V между двумя точками проводника, деленная на силу тока I в проводнике, постоянна и не зависит от V или I. Отношение

называется сопротивлением проводника на участке между двумя точками. Сопротивление измеряется в омах (Ом), если разность потенциалов V выражена в вольтах, а сила тока I – в амперах. Сопротивление металлического проводника пропорционально его длине l и обратно пропорционально площади А его поперечного сечения. Оно остается постоянным, пока постоянна его температура. Обычно эти положения выражают формулой

где r – удельное сопротивление (ОмЧм), зависящее от материала проводника и его температуры. Температурный коэффициент удельного сопротивления определяется как относительное изменение величины r при изменении температуры на один градус. В таблице приведены значения удельных сопротивлений и температурных коэффициентов сопротивления некоторых обычных материалов, измеренные при комнатной температуре. Удельные сопротивления чистых металлов, как правило, ниже, чем у сплавов, а температурные коэффициенты – выше. Удельное сопротивление диэлектриков, особенно серы и слюды, намного выше, чем металлов; отношение достигает величины 1023. Температурные коэффициенты диэлектриков и полупроводников отрицательны и имеют относительно большие значения.
|
УДЕЛЬНЫЕ СОПРОТИВЛЕНИЯ И ТЕМПЕРАТУРНЫЕ КОЭФФИЦИЕНТЫ ОБЫЧНЫХ МАТЕРИАЛОВ ПРИ КОМНАТНОЙ ТЕМПЕРАТУРЕ |
||
| Элемент |
Удельное сопротивление, |
Температурный коэффициент, 1/° С |
| Серебро |
1,6Ч10–8 |
4,0Ч10–3 |
| Золото |
2,2Ч10–8 |
3,7Ч10–3 |
| Медь |
1,7Ч10–8 |
4,0Ч10–3 |
| Алюминий |
2,7Ч10–8 |
4,2Ч10–3 |
| Вольфрам |
5,3Ч10–8 |
4,6Ч10–3 |
| Никель |
7,0Ч10–8 |
6,1Ч10–3 |
| Углерод |
3,5Ч10–3 |
–0,03 |
| Сера |
1015 |
|
| Сплав или соединение |
Удельное сопротивление, |
Температурный коэффициент, 1/°С |
| Константан 45 Ni–55 Cu |
49Ч10–8 |
0,5Ч10–5 |
| Нихром Ni–Cr–Fe |
112Ч10–8 |
40,0Ч10–5 |
| Бакелит |
1010 |
–0,06 |
| Стекло |
1012 |
–0,07 |
| Слюда |
1015 |
–0,07 |
Тепловое действие электрического тока.
Тепловое действие электрического тока впервые наблюдалось в 1801, когда током удалось расплавить различные металлы. Первое промышленное применение этого явления относится к 1808, когда был предложен электрозапал для пороха. Первая угольная дуга, предназначенная для обогрева и освещения, была выставлена в Париже в 1802. К полюсам вольтова столба, насчитывавшего 120 элементов, подсоединялись электроды из древесного угля, и когда оба угольных электрода приводились в соприкосновение, а затем разводились, возникал «сверкающий разряд исключительной яркости».
Исследуя тепловое действие электрического тока, Дж.Джоуль (1818–1889) провел эксперимент, который подвел прочную основу под закон сохранения энергии. Джоуль впервые показал, что химическая энергия, которая расходуется на поддержание в проводнике тока, приблизительно равна тому количеству тепла, которое выделяется в проводнике при прохождении тока. Он установил также, что выделяющееся в проводнике тепло пропорционально квадрату силы тока. Это наблюдение согласуется как с законом Ома (V = IR), так и с определением разности потенциалов (V = W/q). В случае постоянного тока за время t через проводник проходит заряд q = It. Следовательно, электрическая энергия, превратившаяся в проводнике в тепло, равна:

Эта энергия называется джоулевым теплом и выражается в джоулях (Дж), если ток I выражен в амперах, R – в омах, а t – в секундах.
Источники электрической энергии для цепей постоянного тока.
При протекании по цепи постоянного электрического тока происходит столь же постоянное превращение электрической энергии в тепло. Для поддержания тока необходимо, чтобы на некоторых участках цепи вырабатывалась электрическая энергия. Вольтов столб и другие химические источники тока преобразуют химическую энергию в электрическую. В последующих разделах обсуждаются и другие устройства, вырабатывающие электрическую энергию. Все они действуют наподобие электрических «насосов», перемещающих электрические заряды против действия сил, содаваемых постоянным электрическим полем.
Важным параметром источника тока является электродвижущая сила (ЭДС). ЭДС источника тока определяется как разность потенциалов на его зажимах в отсутствие тока (при разомкнутой внешней цепи) и измеряется в вольтах.
Термоэлектричество.
В 1822 Т.Зеебек обнаружил, что в цепи, составленной из двух разных металлов, возникает ток, если одна точка их соединения горячее другой. Подобная цепь называется термоэлементом. В 1834 Ж.Пельтье установил, что при прохождении тока через спай двух металлов в одном направлении тепло поглощается, а в другом – выделяется. Величина этого обратимого эффекта зависит от материалов спая и его температуры. Каждый спай термоэлемента обладает ЭДС ej = Wj/q, где Wj – тепловая энергия, превращающаяся в электрическую при одном направлении перемещения заряда q, или электрическая энергия, превращающаяся в тепло при перемещении заряда в другом направлении. Эти ЭДС противоположны по направлению, но обычно не равны одна другой, если температуры спаев различаются.
У.Томсон (1824–1907) установил, что полная ЭДС термоэлемента складывается не из двух, а из четырех ЭДС. В дополнение к ЭДС, возникающим в спаях, имеются две дополнительные ЭДС, обусловленные перепадом температуры на проводниках, образующих термоэлемент. Им было дано название ЭДС Томсона.
Эффекты Зеебека и Пельтье.
Термоэлемент представляет собой «тепловую машину», в определенном отношении сходную с генератором тока, приводимым в действие паровой турбиной, но без движущихся частей. Подобно турбогенератору, он превращает тепло в электроэнергию, отбирая его от «нагревателя» с более высокой температурой и отдавая часть этого тепла «холодильнику» с более низкой температурой. В термоэлементе, действующем подобно тепловой машине, «нагреватель» находится у горячего спая, а «холодильник» – у холодного. То обстоятельство, что тепло с более низкой температурой теряется, ограничивает теоретический кпд преобразования тепловой энергии в электрическую значением (T1 – T2)/T1 где T1 и T2 – абсолютные температуры «нагревателя» и «холодильника». Дополнительное снижение кпд термоэлемента обусловлено потерей тепла за счет теплопередачи от «нагревателя» к «холодильнику».
См. ТЕПЛОТА; ТЕРМОДИНАМИКА.
Преобразование тепла в электрическую энергию, происходящее в термоэлементе, обычно называют эффектом Зеебека. Термоэлементы, называемые термопарами, применяют для измерения температуры, особенно в труднодоступных местах. Если один спай находится в контролируемой точке, а другой – при комнатной температуре, которая известна, то термо-ЭДС служит мерой температуры в контролируемой точке. Большие успехи достигнуты в области применения термоэлементов для прямого преобразования тепла в электроэнергию в промышленных масштабах.
Если через термоэлемент пропускать ток от внешнего источника, то холодный спай будет поглощать тепло, а горячий – выделять его. Такое явление называется эффектом Пельтье. Этот эффект можно использовать либо для охлаждения с помощью холодных спаев, либо для обогрева горячими спаями. Тепловая энергия, выделяемая горячим спаем, больше полного количества тепла, подведенного к холодному спаю, на величину, соответствующую подведенной электрической энергии. Таким образом, горячий спай выделяет больше тепла, чем соответствовало бы полному количеству электрической энергии, подведенной к устройству. В принципе большое число последовательно соединенных термоэлементов, холодные спаи которых выведены наружу, а горячие находятся внутри помещения, можно использовать в качестве теплового насоса, перекачивающего тепло из области с более низкой температурой в область с более высокой температурой. Теоретически выигрыш в тепловой энергии по сравнению с затратами электрической энергии может составлять T1/(T1 – T2).
К сожалению, для большинства материалов эффект настолько мал, что на практике потребовалось бы слишком много термоэлементов. Кроме того, применимость эффекта Пельтье несколько ограничивает теплопередача от горячего спая к холодному за счет теплопроводности в случае металлических материалов. Исследования полупроводников привели к созданию материалов с достаточно большими эффектами Пельтье для ряда практических применений. Эффект Пельтье оказывается особенно ценным при необходимости охлаждать труднодоступные участки, где непригодны обычные способы охлаждения. С помощью таких устройств охлаждают, например, приборы в космических кораблях.
Электрохимические эффекты.
В 1842 Г.Гельмгольц продемонстрировал, что в источнике тока типа вольтова столба химическая энергия превращается в электрическую, а в процессе электролиза электрическая энергия превращается в химическую. Химические источники тока типа сухих элементов (обычных батареек) и аккумуляторов оказались чрезвычайно практичными. При зарядке аккумуляторной батареи электрическим током оптимальной величины бóльшая часть сообщенной ей электрической энергии превращается в химическую энергию, которая может быть использована при разрядке аккумулятора. И при зарядке, и при разрядке аккумулятора часть энергии теряется в виде тепла; эти тепловые потери обусловлены внутренним сопротивлением аккумулятора. ЭДС такого источника тока равна разности потенциалов на его зажимах в условиях разомкнутой цепи, когда отсутствует падение напряжения IR на внутреннем сопротивлении.
Цепи постоянного тока.
Для расчета силы постоянного тока в простой цепи можно использовать закон, открытый Омом при исследовании вольтова столба:

где R – сопротивление цепи и V – ЭДС источника.
Если несколько резисторов с сопротивлениями R1, R2 и т.д. соединены последовательно, то в каждом из них ток I одинаков и полная разность потенциалов равна сумме отдельных разностей потенциалов (рис. 1,а). Общее сопротивление можно определить как сопротивление Rs последовательного соединения группы резисторов. Разность потенциалов на этой группе равна

следовательно,

Если резисторы соединены параллельно, то разность потенциалов на группе совпадает с разностью потенциалов на каждом отдельном резисторе (рис. 1,б). Полный ток через группу резисторов равен сумме токов через отдельные резисторы, т.е.

Поскольку I1 = V/R1, I2 = V/R2, I3 = V/R3 и т.д., сопротивление параллельного соединения группы Rp определяется соотношением

откуда следует

При решении задач с цепями постоянного тока любого типа нужно сначала по возможности упростить задачу, пользуясь соотношениями (9) и (10).
Законы Кирхгофа.
Г.Кирхгоф (1824–1887) детально исследовал закон Ома и разработал общий метод расчета постоянных токов в электрических цепях, в том числе содержащих несколько источников ЭДС. Этот метод основан на двух правилах, называемых законами Кирхгофа:
1. Алгебраическая сумма всех токов в любом узле цепи равна нулю.
2. Алгебраическая сумма всех разностей потенциалов IR в любом замкнутом контуре равна алгебраической сумме всех ЭДС в этом замкнутом контуре.
Этих двух законов достаточно для решения любой задачи, связанной с цепями постоянного тока.
См. также БАТАРЕЯ ЭЛЕКТРОПИТАНИЯ; ЭЛЕКТРИЧЕСКИЕ ЦЕПИ.
МАГНИТОСТАТИКА
Магнитостатика имеет дело с силами, возникающими между телами с постоянным намагничением.
О свойствах природных магнитов сообщается в трудах Фалеса Милетского (прибл. 600 до н.э.) и Платона (427–347 до н.э.). Слово «магнит» возникло в связи с тем, что природные магниты были обнаружены греками в Магнесии (Фессалия). К 11 в. относится сообщение китайцев Шен Куа и Чу Ю об изготовлении компасов из природных магнитов и использовании их в навигации. Если длинная игла из природного магнита уравновешена на оси, позволяющей ей свободно поворачиваться в горизонтальной плоскости, то она всегда обращена одним концом к северу, а другим – к югу. Пометив указывающий на север конец, можно пользоваться таким компасом для определения направлений. Магнитные эффекты концентрировались у концов такой иглы, и поэтому их назвали полюсами (соответственно северным и южным).
Сочинение У.Гильберта О магните (De magnete, 1600) явилось первой известной нам попыткой исследования магнитных явлений с позиций науки. В этом труде собраны имевшиеся тогда сведения об электричестве и магнетизме, а также результаты собственных экспериментов автора.
Стержни из железа, стали и некоторых других материалов намагничиваются при соприкосновении с природными магнитами, а их способность притягивать небольшие кусочки железа, как и у природных магнитов, обычно проявляется вблизи полюсов, располагающихся у концов стержней. Подобно электрическим зарядам, полюса бывают двух типов. Одинаковые полюса взаимно отталкиваются, а противоположные – притягиваются. Каждый магнит имеет два одинаковых по силе полюса противоположного знака. В отличие от электрических зарядов, которые можно отделить друг от друга, пары полюсов оказались неразделимы. Если намагниченный стержень аккуратно распилить посередине между полюсами, то появляются два новых полюса той же силы. Поскольку электрические заряды не влияют на магнитные полюса и наоборот, электрические и магнитные явления долгое время считались совершенно разными по своей природе.
Кулон установил закон для сил притяжения и отталкивания полюсов, воспользовавшись весами, похожими на те, что он применял, выясняя закон для сил, действующих между двумя точечными зарядами. Оказалось, что сила, действующая между точечными полюсами, пропорциональна их «величине» и обратно пропорциональна квадрату расстояния между ними. Этот закон записывается в виде

где p и pў – «величины» полюсов, r – расстояние между ними, а Km – коэффициент пропорциональности, который зависит от используемых единиц измерения. В современной физике от рассмотрения величин магнитных полюсов отказались (по причинам, которые объясняются в следующем разделе), так что этот закон представляет в основном исторический интерес.
МАГНИТНЫЕ ЭФФЕКТЫ ЭЛЕКТРИЧЕСКОГО ТОКА
В 1820 Г.Эрстед (1777–1851) обнаружил, что проводник с током воздействует на магнитную стрелку, поворачивая ее. Буквально неделей позже Ампер показал, что два параллельных проводника с током одного направления притягиваются друг к другу. Позднее он высказал предположение, что все магнитные явления обусловлены токами, причем магнитные свойства постоянных магнитов связаны с токами, постоянно циркулирующими внутри этих магнитов. Это предположение полностью соответствует современным представлениям.
См. МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА.
Электрические поля, создаваемые электрическими зарядами в окружающем пространстве, характеризуются силой, действующей на единичный пробный заряд. Вокруг намагниченных материалов и проводников с электрическим током возникают магнитные поля, которые первоначально характеризовали силой, действующей на «единичный» пробный полюс. Хотя такой способ определения напряженности магнитного поля теперь не применяется, этот подход сохранился при определении направления магнитного поля. Если маленькая магнитная стрелка подвешена в своем центре масс и может свободно вращаться в любом направлении, то ее ориентация и будет указывать направление магнитного поля.
От использования магнитных полюсов для определения характеристик магнитных полей пришлось отказаться по ряду причин: во-первых, нельзя изолировать отдельный полюс; во-вторых, ни положение, ни величину полюса нельзя точно определить; в-третьих, магнитные полюса – по существу, фиктивные понятия, поскольку на самом деле магнитные эффекты обусловлены движением электрических зарядов. Соответственно этому магнитные поля теперь характеризуют силой, с которой они действуют на проводники с током. На рис. 2 изображен проводник с током I, лежащий в плоскости рисунка; направление тока I указано стрелкой. Проводник находится в однородном магнитном поле, направление которого параллельно плоскости рисунка и составляет угол f с направлением проводника с током. Величина индукции магнитного поля B дается выражением

где F – сила, с которой поле b действует на элемент проводника длиной l с током I. Направление силы F перпендикулярно как направлению магнитного поля, так и направлению тока. На рис. 2 эта сила перпендикулярна плоскости рисунка и направлена от читателя. Величину B в принципе можно определить, поворачивая проводник, пока F не достигнет максимального значения, при котором B = Fмакс/Il. Направление магнитного поля тоже можно установить, поворачивая проводник, пока сила F не обратится в нуль, т.е. проводник окажется параллельным B. Хотя эти правила трудно применять на практике, экспериментальные методы определения величины и направления магнитных полей основаны на них. Силу, действующую на проводник с током, обычно записывают в виде

Ж.Био (1774–1862) и Ф.Савар (1791–1841) вывели закон, позволяющий вычислять магнитное поле, создаваемое известным распределением электрических токов, а именно

где B – магнитная индукция, создаваемая элементом проводника малой длины l с током I. Направление магнитного поля, создаваемого этим элементом тока, показано на рис. 3, где поясняются также величины r и f. Коэффициент пропорциональности k зависит от выбора единиц измерения. Если I выражается в амперах, l и r – в метрах, а B – в теслах (Тл), то k = m0/4p = 10–7 Гн/м. Для определения величины и направления B в любой точке пространства, которое создает проводник большой длины и произвольной формы, следует мысленно разбить проводник на короткие отрезки, вычислить величины b и определить направление полей, создаваемых отдельными отрезками, а затем векторно сложить эти отдельные поля. Например, если ток I в проводнике, образующем окружность радиусом a, направлен по часовой стрелке, то поле в центре окружности легко вычисляется. В формуле (13) расстояние r от каждого элемента проводника до центра окружности равно a и f = 90°. Кроме того, поле, создаваемое каждым элементом, перпендикулярно плоскости окружности и направлено от читателя. Сложив все поля, получим магнитную индукцию в центре:

Чтобы найти поле вблизи проводника, создаваемое очень длинным прямолинейным проводником с током I, для суммирования полей потребуется прибегнуть к интегрированию. Найденное таким способом поле равно:

где r – расстояние по перпендикуляру от проводника. Это выражение используется в принятом в настоящее время определении ампера.
Гальванометры.
Соотношение (12) позволяет сравнивать силы электрических токов. Созданный для этой цели прибор носит название гальванометра. Первый такой прибор был построен И.Швайгером в 1820. Он представлял собой катушку провода, внутри которой подвешена магнитная стрелка. Измеряемый ток пропускался через катушку и создавал вокруг стрелки магнитное поле. На стрелку действовал вращающий момент, пропорциональный силе тока, который уравновешивался за счет упругости нити подвеса. Магнитное поле Земли вносит искажения, однако его влияние можно исключить, окружив стрелку постоянными магнитами. В 1858 У.Томсон, более известный как лорд Кельвин, прикрепил к стрелке зеркальце и ввел ряд других усовершенствований, значительно повысивших чувствительность гальванометра. Подобные гальванометры относятся к классу приборов с подвижной стрелкой.
Хотя гальванометр с подвижной стрелкой можно сделать чрезвычайно чувствительным, его почти полностью вытеснил прибор с подвижной катушкой или рамкой, помещенной между полюсами постоянного магнита. Магнитное поле большого подковообразного магнита в гальванометре оказывается столь сильным по сравнению с магнитным полем Земли, что влиянием последнего можно пренебречь (рис. 4). Гальванометр с подвижной рамкой был предложен в 1836 У.Стердженом (1783–1850), но не получил должного признания, пока в 1882 Ж.Д'Арсонваль не создал современный вариант этого прибора.
Электромагнитная индукция.
После того как Эрстед установил, что постоянный ток создает вращающий момент, действующий на магнит, делалось множество попыток обнаружить ток, вызванный присутствием магнитов. Однако магниты были слишком слабыми, а методы измерения тока – слишком грубыми для обнаружения какого-либо эффекта. Наконец, два исследователя – Дж.Генри (1797–1878) в Америке и М.Фарадей (1791–1867) в Англии – в 1831 независимо друг от друга обнаружили, что при изменении магнитного поля в находящихся рядом проводящих цепях возникают кратковременные токи, но эффект отсутствует, если магнитное поле остается постоянным.
Фарадей считал, что не только электрические, но и магнитные поля – это силовые линии, заполняющие пространство. Числу силовых линий магнитного поля, пересекающих произвольную поверхность s, соответствует величина F, которая называется магнитным потоком:

где Bn – проекция магнитного поля B на нормаль к элементу площади ds. Единица измерения магнитного потока называется вебером (Вб); 1 Вб = 1 ТлЧм2.
Фарадеем был сформулирован закон об ЭДС, наводимой в замкнутом витке провода изменяющимся магнитным полем (закон магнитной индукции). Согласно этому закону, такая ЭДС пропорциональна скорости изменения полного магнитного потока через виток. В системе единиц СИ коэффициент пропорциональности равен 1 и, таким образом, ЭДС (в вольтах) равна скорости изменения магнитного потока (в Вб/с). Математически это выражается формулой

где знак минус показывает, что магнитные поля токов, создаваемых этой ЭДС, направлены так, что уменьшают изменение магнитного потока. Это правило для определения направления наводимой ЭДС согласуется с более общим правилом, сформулированным в 1833 Э.Ленцем (1804–1865): наведенная ЭДС направлена так, что противодействует вызывающей ее появление причине. В случае замкнутой цепи, в которой возникает ток, это правило можно вывести непосредственно из закона сохранения энергии; этим правилом определяется направление наводимой ЭДС и в случае разомкнутой цепи, когда индукционный ток не возникает.
Если катушка состоит из N витков провода, каждый из которых пронизывается магнитным потоком F, то

Это соотношение справедливо независимо от того, по какой причине изменяется пронизывающий цепь магнитный поток.
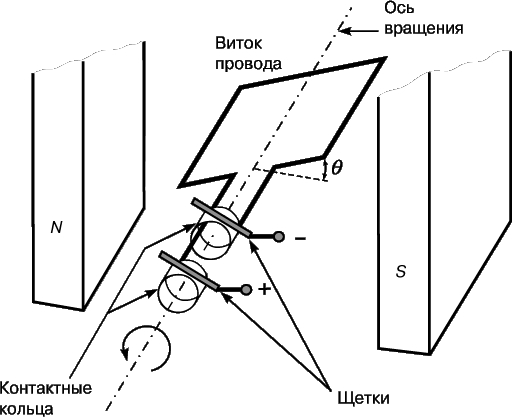
Генераторы.
Принцип действия электромашинного генератора показан на рис. 5. Прямоугольный виток провода вращается против часовой стрелки в магнитном поле между полюсами магнита. Концы витка выведены наружу к контактным кольцам и подключены к внешней цепи через контактные щетки. Когда плоскость витка перпендикулярна полю, пронизывающий петлю магнитный поток максимален. Если же плоскость витка параллельна полю, то магнитный поток равен нулю. Когда плоскость витка снова оказывается перпендикулярной полю, повернувшись на 180°, магнитный поток через виток максимален в противоположном направлении. Таким образом, при вращении витка пронизывающий его магнитный поток непрерывно меняется и в соответствии с законом Фарадея меняется напряжение на зажимах.
Чтобы проанализировать, что происходит в простом генераторе переменного тока, будем считать магнитный поток положительным, когда угол q находится в интервале от 0° до 180°, и отрицательным, когда q составляет от 180° до 360°. Если B – индукция магнитного поля и A – площадь витка, то магнитный поток через виток будет равен:

Если виток вращается с частотой f об./с (т.е. 2pf рад/с), то спустя время t с момента начала вращения, когда q было равно 0, получим q = 2pft рад. Таким образом, выражение для потока через виток приобретает вид

Согласно закону Фарадея, наводимое напряжение получается дифференцированием потока:

Знаки у щеток на рисунке показывают полярность наводимого напряжения в соответствующий момент. Косинус изменяется от +1 до -1, так что величина 2pfAB есть просто амплитуда напряжения; можно обозначить ее через  и записать
и записать

(При этом мы опустили знак «минус», заменив его соответствующим выбором полярности выводов генератора на рис 5.) На рис. 6 представлен график изменения напряжения  по времени.
по времени.
Напряжение, вырабатываемое описанным простым генератором, периодически меняет свое направление на обратное; то же относится к токам, создаваемым в электрических цепях этим напряжением. Такой генератор называют генератором переменного тока.
Ток, всегда сохраняющий одно и то же направление, называется постоянным. В некоторых случаях, например для зарядки аккумуляторов, необходим такой ток. Можно двумя способами получать постоянный ток из переменного. Один состоит в том, что во внешнюю цепь включают выпрямитель, пропускающий ток только в одном направлении. Это позволяет как бы выключать генератор на один полупериод и включать его только в тот полупериод, когда напряжение имеет нужную полярность. Другой способ – переключать контакты, соединяющие виток с внешней цепью, через каждый полупериод, когда напряжение меняет полярность. Тогда ток во внешней цепи всегда будет направлен в одну сторону, хотя напряжение, наводимое в витке, меняет свою полярность. Переключение контактов осуществляется с помощью коллекторных полуколец, установленных вместо токосъемных колец, как показано на рис. 7,а. Когда плоскость витка вертикальна, скорость изменения магнитного потока и, следовательно, наводимое напряжение падают до нуля. Именно в этот момент щетки проскальзывают над зазором, разделяющим два полукольца, и происходит переключение внешней цепи. Напряжение, возникающее во внешней цепи, изменяется так, как показано на рис. 7,б.
См. также ЭЛЕКТРОМАШИННЫЕ ГЕНЕРАТОРЫ И ЭЛЕКТРОДВИГАТЕЛИ.
Взаимная индукция.
Если две замкнутые катушки провода расположены рядом, но электрически не связаны друг с другом, то при изменении тока в одной из них в другой наводится ЭДС. Поскольку магнитный поток через вторую катушку пропорционален току в первой катушке, изменение этого тока влечет за собой изменение магнитного потока с наведением соответствующей ЭДС. Катушки можно поменять ролями, и тогда при изменении тока во второй катушке будет наводиться ЭДС в первой. ЭДС, наводимая в одной катушке, определяется скоростью изменения тока в другой и зависит от размеров и числа витков каждой катушки, а также от расстояния между катушками и их ориентации одна относительно другой. Эти зависимости сравнительно просты, если поблизости не располагаются магнитные материалы. Отношение ЭДС, наведенной в одной катушке, к скорости изменения тока в другой называется коэффициентом взаимоиндукции двух катушек, отвечающей их данному расположению. Если наведенная ЭДС выражается в вольтах, а скорость изменения тока – в амперах за секунду (А/с), то взаимоиндукция будет выражена в генри (Гн). ЭДС, наводимые в катушках, даются следующими формулами:

где M – коэффициент взаимоиндукции двух катушек. Катушку, подключенную к источнику тока, принято называть первичной катушкой или обмоткой, а другую – вторичной. Постоянный ток в первичной обмотке не создает напряжения во вторичной, хотя в момент включения и выключения тока во вторичной обмотке кратковременно возникает ЭДС. Но если к первичной обмотке подключается ЭДС, создающая в этой обмотке переменный ток, то переменная ЭДС наводится и во вторичной обмотке. Таким образом, вторичная обмотка может питать переменным током активную нагрузку или другие схемы без прямого подключения их к источнику ЭДС.
Трансформаторы.
Взаимоиндукцию двух обмоток можно значительно увеличить, намотав их на общий сердечник из ферромагнитного материала, такого, как железо. Подобное устройство называется трансформатором. В современных трансформаторах ферромагнитный сердечник образует замкнутую магнитную цепь, так что почти весь магнитный поток проходит внутри сердечника и, следовательно, через обе обмотки. Источник переменной ЭДС, подключенный к первичной обмотке, создает в железном сердечнике переменный магнитный поток. Этот поток наводит переменные ЭДС и в первичной, и во вторичной обмотках, причем максимальные значения каждой ЭДС пропорциональны числу витков в соответствующей обмотке. В хороших трансформаторах сопротивление обмоток настолько мало, что ЭДС, наведенная в первичной обмотке, почти совпадает с приложенным напряжением, а разность потенциалов на выводах вторичной обмотки почти совпадает с наведенной в ней ЭДС.
Таким образом, отношение падения напряжения на нагрузке вторичной обмотки к напряжению, приложенному к первичной обмотке, равно отношению чисел витков во вторичной и первичной обмотках, что обычно записывают в виде равенства

где V1 – падение напряжения на N1 витках первичной обмотки, а V2 – падение напряжения на N2 витках вторичной обмотки. В зависимости от соотношения чисел витков в первичной и вторичной обмотках различают повышающие и понижающие трансформаторы. Отношение N2/N1 больше единицы в повышающих трансформаторах и меньше единицы в понижающих. Благодаря трансформаторам возможна экономичная передача электрической энергии на большие расстояния.
См. также ТРАНСФОРМАТОР ЭЛЕКТРИЧЕСКИЙ.
Самоиндукция.
Электрический ток в отдельной катушке также создает магнитный поток, который пронизывает саму эту катушку. Если ток в катушке изменяется со временем, то будет изменяться и магнитный поток через катушку, наводя в ней ЭДС точно так же, как это происходит при работе трансформатора. Возникновение ЭДС в катушке при изменении тока в ней называется самоиндукцией. Самоиндукция влияет на ток в катушке аналогично тому, как влияет инерция на движение тел в механике: она замедляет установление постоянного тока в цепи при его включении и препятствует его мгновенному прекращению при выключении. Она также служит причиной возникновения искр, проскакивающих между контактами выключателей при размыкании цепи. В цепи переменного тока самоиндукция создает реактивное сопротивление, ограничивающее амплитуду тока.
В отсутствие магнитных материалов вблизи неподвижной катушки магнитный поток, пронизывающий ее, пропорционален току в цепи. Согласно закону Фарадея (16), ЭДС самоиндукции должна в этом случае быть пропорциональна скорости изменения тока, т.е.

где L – коэффициент пропорциональности, называемый самоиндукцией или индуктивностью цепи. Формулу (18) можно рассматривать как определение величины L. Если наводимая в катушке ЭДС  выражается в вольтах, ток i – в амперах и время t – в секундах, то L будет измеряться в генри (Гн). Знак «минус» указывает на то, что наводимая ЭДС противодействует увеличению тока i, как и следует из закона Ленца. Внешняя ЭДС, преодолевающая ЭДС самоиндукции, должна иметь знак «плюс». Поэтому в цепях переменного тока падение напряжения на индуктивности равно Ldi/dt.
выражается в вольтах, ток i – в амперах и время t – в секундах, то L будет измеряться в генри (Гн). Знак «минус» указывает на то, что наводимая ЭДС противодействует увеличению тока i, как и следует из закона Ленца. Внешняя ЭДС, преодолевающая ЭДС самоиндукции, должна иметь знак «плюс». Поэтому в цепях переменного тока падение напряжения на индуктивности равно Ldi/dt.
ПЕРЕМЕННЫЕ ТОКИ
Как уже говорилось, переменные токи – это токи, направление которых периодически изменяется. Число периодов циклического изменения тока в секунду называется частотой переменного тока и измеряется в герцах (Гц). Электроэнергия обычно подается потребителю в виде переменного тока с частотой 50 Гц (в России и в европейских странах) или 60 Гц (в США).
Поскольку переменный ток изменяется во времени, простые способы решения задач, пригодные для цепей постоянного тока, здесь непосредственно неприменимы. При очень высоких частотах заряды могут совершать колебательное движение – перетекать из одних мест цепи в другие и обратно. При этом, в отличие от цепей постоянного тока, токи в последовательно соединенных проводниках могут оказаться неодинаковыми. Емкости, присутствующие в цепях переменного тока, усиливают этот эффект. Кроме того, при изменении тока сказываются эффекты самоиндукции, которые становятся существенными даже при низких частотах, если используются катушки с большой индуктивностью. При сравнительно низких частотах цепи переменного тока можно по-прежнему рассчитывать с помощью правил Кирхгофа, которые, однако, необходимо соответствующим образом модифицировать.
Цепь, в которую входят разные резисторы, катушки индуктивности и конденсаторы, можно рассматривать, как если бы она состояла из обобщенных резистора, конденсатора и катушки индуктивности, соединенных последовательно. Рассмотрим свойства такой цепи, подключенной к генератору синусоидального переменного тока (рис. 8). Чтобы сформулировать правила, позволяющие рассчитывать цепи переменного тока, нужно найти соотношение между падением напряжения и током для каждого из компонентов такой цепи.
Конденсатор играет совершенно разные роли в цепях переменного и постоянного токов. Если, например, к цепи на рис. 8 подключить электрохимический элемент, то конденсатор начнет заряжаться, пока напряжение на нем не станет равным ЭДС элемента. Затем зарядка прекратится и ток упадет до нуля. Если же цепь подключена к генератору переменного тока, то в один полупериод электроны будут вытекать из левой обкладки конденсатора и накапливаться на правой, а в другой – наоборот. Эти перемещающиеся электроны и представляют собой переменный ток, сила которого одинакова по обе стороны конденсатора. Пока частота переменного тока не очень велика, ток через резистор и катушку индуктивности также одинаков.
Реактивное и полное сопротивления.
Чтобы проанализировать соотношение между током и напряжением для контура, изображенного на рис. 8, предположим, что заряд на левой пластине конденсатора дается выражением
 ,
,
а заряд на правой пластине равен – q. Здесь Q – максимальный заряд (Кл), t – время (с), а w = 2pf, где f – частота переменного тока (Гц). Ток через каждый элемент цепи равен:

где максимальный ток Iмакс равен w Q. Переменное падение напряжения на конденсаторе равно:

Согласно закону Ома, падение напряжения на резисторе дается выражением

Падение напряжения всей цепи от a до b равно:

или

где

причем

Величина XL называется индуктивным сопротивлением и выражается в омах, если L – в генри; величина XC называется емкостным сопротивлением и выражается в омах, если C – в фарадах. Полное реактивное сопротивление цепи X также выражается в омах. Формулу (19) можно привести к простому и более ясному виду, использовав тригонометрическое тождество cos (a + b) = cos a cos b – sin a sin b. Поскольку R и X выражены в омах, их можно рассматривать как катеты прямоугольного треугольника для определения угла q (рис. 9). Гипотенуза

называется полным сопротивлением (импедансом) последовательного соединения. На рис. 9 изображен треугольник полного сопротивления, из которого явствует, что R = Z cos q, X = Z sin q и tg q = X/R. Выражение (19) можно переписать в виде v = IмаксZ (cos q cos w t – sin q sin w t), что сводится к выражению

если использовать вышеприведенное тригонометрическое тождество; выражение (21) можно переписать в виде

где

Из формулы (21) следует, что напряжение v на зажимах цепи максимально при t = -q/w, тогда как ток i максимален при t = 0, т.е. ток отстает по фазе от напряжения на угол q. Таким образом, ток отстает по фазе от напряжения, если преобладает индуктивное сопротивление, т.е. если XL больше XC. Ток опережает напряжение, если преобладает емкостное сопротивление, т.е. XC больше XL. Отметим, что соотношение (22) отличается от закона Ома лишь тем, что в нем активное сопротивление R заменено полным сопротивлением Z.
Если сопротивление R и максимальное падение напряжения на зажимах цепи поддерживаются постоянными, то наибольшее значение максимального тока Iмакс отвечает равенству двух реактивных сопротивлений. Если индуктивность и емкость тоже постоянны, то можно добиться равенства их реактивных сопротивлений, изменяя частоту переменного тока. Это достигается при круговой частоте

в таком случае говорят о резонансной настройке цепи.
Выше предполагалось, что переменный ток в цепи установился. В действительности же при подключении цепи к источнику переменного напряжения в ней возникают переходные процессы. Если сопротивление цепи не пренебрежимо мало, переходные токи выделяют свою энергию в виде тепла в резисторе и достаточно быстро затухают, после чего устанавливается стационарный режим переменного тока, что и предполагалось выше. Во многих случаях переходными процессами в цепях переменного тока можно пренебречь. Если же их необходимо учитывать, то нужно исследовать дифференциальное уравнение, описывающее зависимость тока от времени.
Эффективные значения.
Главная задача первых районных электростанций состояла в том, чтобы обеспечивать нужный накал нитей осветительных ламп. Поэтому встал вопрос об эффективности использования для этих цепей постоянного и переменного токов. Согласно формуле (7), для электрической энергии, преобразующейся в тепло в резисторе, тепловыделение пропорционально квадрату силы тока. В случае переменного тока тепловыделение непрерывно колеблется вместе с мгновенным значением квадрата силы тока. Если ток меняется по синусоидальному закону, то усредненное по времени значение квадрата мгновенного тока равно половине квадрата максимального тока, т.е.

Квадратный корень из этой величины называется эффективным значением переменного тока. Следовательно, эффективное значение силы переменного тока равно:

Таким должен быть постоянный ток, чтобы обеспечить тот же нагрев нити накала, что и переменный ток с амплитудой Iмакс. Очевидно, что амплитуда переменного напряжения на лампе накаливания должна быть в  раз больше соответствующего постоянного напряжения. Таким образом, эффективное значение напряжения переменного тока определяется как
раз больше соответствующего постоянного напряжения. Таким образом, эффективное значение напряжения переменного тока определяется как

Согласно формуле (22), полное сопротивление цепи переменного тока равно:

В отсутствие в цепи реактивных элементов имеем Z = R и R = V/I, откуда видно, что соотношение между эффективными значениями напряжения и тока в цепи переменного тока оказывается таким же, как и в цепи постоянного тока.
Мощность, поступающая в последовательную цепь, выраженная через эффективные значения тока и напряжения, равна:

Поскольку мощность, выделяемая в цепи постоянного тока, составляет P = VI, величина cos q называется коэффициентом мощности. Но V = IZ, а R = Z cos q (рис. 9). Таким образом, мощность, выделяемая переменным током в последовательной цепи, равна:

откуда видно, что вся мощность расходуется на нагревание резистора, тогда как в конденсаторе и индуктивности мощность не поглощается. Правда, реальные катушки индуктивности все же поглощают некоторую мощность, особенно если у них имеется железный сердечник. При непрерывном перемагничивании железный сердечник нагревается – частично наводимыми в железе токами, а частично за счет внутреннего трения (гистерезиса), которое препятствует перемагничиванию. Кроме того, индуктивность может наводить токи в расположенных поблизости схемах. При измерениях в цепях переменного тока все эти потери выглядят как потери мощности в сопротивлении. Поэтому сопротивление одной и той же цепи для переменного тока обычно несколько больше, чем для постоянного, и его определяют через потери мощности:

Чтобы электростанция работала экономично, тепловые потери в линии электропередачи (ЛЭП) должны быть достаточно низкими. Если Pc – мощность, поставляемая потребителю, то Pc = VcI как для постоянного, так и для переменного тока, поскольку при надлежащем расчете величину cos q можно сделать равной единице. Потери в ЛЭП составят Pl = RlI2 = RlPc2/Vc2. Поскольку для ЛЭП требуются по крайней мере два проводника длиной l, ее сопротивление Rl = r 2l/A. В этом случае потери в линии

Если проводники выполнены из меди, удельное сопротивление r которой минимально, то в числителе не остается величин, которые можно было бы значительно уменьшить. Единственный практический путь снижения потерь – увеличивать Vc2, поскольку применение проводников с большой площадью поперечного сечения A невыгодно. Это означает, что мощность следует передавать, используя как можно более высокое напряжение. Обычные электромашинные генераторы тока, приводимые в действие турбинами, не могут вырабатывать очень высокое напряжение, которого не выдерживает их изоляция. Кроме того, сверхвысокие напряжения опасны для обслуживающего персонала. Однако напряжение переменного тока, вырабатываемое электростанцией, можно для передачи по ЛЭП повысить с помощью трансформаторов. На другом конце ЛЭП у потребителя используются понижающие трансформаторы, которые дают на выходе более безопасное и практичное низкое напряжение. В настоящее время напряжение в ЛЭП достигает 750 000 В.
Роджерс Э. Физика для любознательных, т. 3. М., 1971
Орир Дж. Физика, т. 2. М., 1981
Джанколи Д. Физика, т. 2. М., 1989
Ответь на вопросы викторины «Физика»