ПРОИЗВОДНАЯ

Содержание статьи

• Мгновенная скорость.
• Геометрическое значение производной. Касательная к графику функции.
• Дифференцируемость функций.
• Непрерывность функции, имеющей производную. Теорема.
• Производные различных порядков.
• Дифференциалы различных порядков.
• Частная производная.

ПРОИЗВОДНАЯ – производной функции y = f(x), заданной на некотором интервале (a, b) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Производную принято обозначать так:

.

Широко употребляются и другие обозначения:

Предел , где рассматривается только Dx > 0 или только Dx < 0, называется соответственно правой или левой производной функции f в точке x. О функции f, заданной на отрезке [a, b] принято говорить, что она имеет на этом отрезке производную, если она имеет производную в любой точке интервала (a, b) и, кроме того, правую производную в точке a и левую в точке b.

Понятие производной возникло как результат многовековых усилий, направленных на решение таких задач, как задача о проведении касательной к кривой, о вычислении скорости неравномерного движения, задачи о вычислении площади криволинейной фигуры. В работах Исаака Ньютона и Готфрида Вильгельма Лейбница эта деятельность получила определенное теоретическое завершение. Ньютон и Лейбниц создали общие методы дифференцирования и интегрирования функций и доказали важную теорему, носящую их имя, устанавливающую тесную связь между операциями дифференцирования и интегрирования. Однако современное изложение этих вопросов существенно отличается от того, как они излагались во времена Ньютона и Лейбница. Современный математический анализ базируется на понятии предела, которое было дано (наряду с другими важнейшими понятиями – непрерывность, интеграл и т.д.) в работах французского математика Огюстена Луи Коши.

Мгновенная скорость.

Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M0 , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M0, а в некоторый следующий момент t + Dt оказалась в положении M1 – на расстоянии s + Ds от начального положения (см. рис.).

Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds. В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds.

Отношение представляет собой среднюю скорость движения точки за время Dt:

.

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:

.

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt, когда приращение времени стремится к нулю. Так как

,

то.

Геометрическое значение производной. Касательная к графику функции.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления.

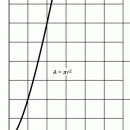
Пусть кривая есть график функции y = f(x) в прямоугольной системе координат (см. рис.).

При некотором значении x функция имеет значение y = f(x). Этим значениям x и y на кривой соответствует точка M0(x, y). Если аргументу x дать приращение Dx, то новому значению аргумента x + Dx соответствует новое значение функции y+Dy = f(x + Dx). Соответствующей ему точкой кривой будет точка M1(x + Dx, y + Dy). Если провести секущую M0M1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что .

Если теперь Dx стремится к нулю, то точка M1 перемещается вдоль кривой, приближаясь к точке M0, и угол j изменяется с изменением Dx. При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:

.

Следовательно, f´(x) = tga

т.е. значение производной f´(x) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке M0(x,y) с положительным направлением оси Ox.

Дифференцируемость функций.

Определение. Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке.

Непрерывность функции, имеющей производную. Теорема.

Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–Ґ < х < Ґ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f(a) = f(b) = 0), то внутри отрезка [a,b] существует, по крайней мере одна, точка x = с, a < c < b, в которой производная fў(x) обращается в нуль, т.е. fў(c) = 0.

Теорема о конечных приращениях (теорема Лагранжа). Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a, b] найдется по крайней мере одна точка с, a < c < b, что

f(b) – f(a) = f ў(c)(b – a).

Теорема об отношении приращений двух функций (теорема Коши). Если f(x) и g(x) – две функции, непрерывные на отрезке [a, b] и дифференцируемые во всех внутренних точках этого отрезка, причем gў(x) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a, b] найдется такая точка x = с, a < c < b, что

.

Производные различных порядков.

Пусть функция y = f(x) дифференцируема на некотором отрезке [a, b]. Значения производной f ў(x), вообще говоря, зависят от x, т.е. производная f ў(x) представляет собой тоже функцию от x. При дифференцировании этой функции получается так называемая вторая производная от функции f(x), которая обозначается f ўў (x).

Производной n-го порядка от функции f(x) называется производная (первого порядка) от производной n-1-го и обозначается символом y(n) = (y(n – 1))ў.

Дифференциалы различных порядков.

Дифференциал функции y = f(x), где x – независимая переменная, есть dy = f ў(x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:

d(dx) = d2y = f ўў(x)(dx)².

Дифференциалом n-го порядка называется первый дифференциал от дифференциала n-1-го порядка:

dⁿy = d(dⁿ–1 y) = f(n)(x)dx(n).

Частная производная.

Если функция зависит не от одного, а от нескольких аргументов x_i (i изменяется от 1 до n, i = 1, 2,… n), f(x1, x2,… x_n), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, x_i . Частная производная 1-ого порядка по x_i определяется как обычная производная, при этом предполагается, что все аргументы, кроме x_i, сохраняют постоянные значения. Для частных производных вводятся обозначения

f_xn, или

Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.

Анна Чугайнова