ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Содержание статьи

• Примеры.
• Броуновское движение.

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ – плотность вероятности распределения частиц макроскопической системы по координатам, импульсам или квантовым состояниям. Функция распределения является основной характеристикой самых разнообразных (не только физических) систем, которым свойственно случайное поведение, т.е. случайное изменение состояния системы и, соответственно, ее параметров. Даже в стационарных внешних условиях само состояние системы может быть таким, что результат измерения некоторого его параметра является случайной величиной. Функция распределения в подавляющем большинстве случаев содержит в себе всю возможную и потому исчерпывающую информацию о свойствах таких систем.

В математической теории вероятностей и математической статистике функция распределения и плотность вероятности отличаются друг от друга, но однозначно связаны между собой. Ниже речь пойдет почти исключительно о плотности вероятности, которую (согласно принятой в физике давней традиции) называют плотностью распределения вероятности или функцией распределения, ставя знак равенства между этими двумя терминами.

Случайное поведение в той или иной мере характерно для всех квантовомеханических систем: элементарные частицы, атомы молекулы и т.п. Однако случайное поведение – это не специфическая черта только квантовомеханических систем, многие чисто классические системы обладают этим свойством.

Примеры.

При бросании монеты на твердую горизонтальную поверхность, неясно, как она ляжет: цифрой вверх или гербом. Известно, что вероятности этих событий, при определенных условиях, равны 1/2. При бросании игральной кости нельзя с уверенностью сказать, какая из шести цифр окажется на верхней грани. Вероятность выпадения каждой из цифр при определенных предположениях (кость – однородный куб без сколотых ребер и вершин падает на твердую, гладкую горизонтальную поверхность) равна 1/6.

Хаотичность движения молекул в наибольшей степени проявляется в газе. Даже в стационарных внешних условиях, флуктуируют (меняются случайным образом) точные значения макроскопических параметров, и только их средние значения при этом постоянны. Описание макроскопических систем на языке средних значений макропараметров и составляет суть термодинамического описания (см. статью ТЕРМОДИНАМИКА).

Пусть есть идеальный одноатомный газ и три его (еще не усредненных) макроскопических параметра: N – число атомов, движущихся внутри сосуда, занятого газом; P –давление газа на стенку сосуда и – внутренняя энергия газа. Газ идеальный и одноатомный, поэтому его внутренняя энергия есть просто сумма кинетических энергий поступательного движения атомов газа.

Число N флуктуирует, по крайней мере, из-за процесса сорбции (прилипания к стенке сосуда при соударении с ней) и десорбции (процесса отлипания, когда молекула отрывается от стенки сама по себе или в результате удара по ней другой молекулы), наконец, процесса образования кластеров – короткоживущих комплексов из нескольких молекул. Если бы Можно было измерять N мгновенно и точно, то полученная зависимость N(t) была бы похожей на изображенную на рисунке.

Размах флуктуаций на рисунке для наглядности сильно завышен, но при небольшом среднем значении (бN с ~ 10²) числа частиц в газе он примерно таким и будет.

Если выбрать маленькую площадку на стенке сосуда измерять силу, действующую на эту площадку в результате ударов молекул газа, находящегося в сосуде, то отношение среднего значения нормальной к площадке компоненты этой силы к площади площадки и принято называть давлением. В разные моменты времени к площадке будет подлетать разное количество молекул, причем с разными скоростями. В результате, если бы можно было измерять эту силу мгновенно и точно, была бы картина, подобная изображенной на рисунке, нужно только изменить обозначения по вертикальной оси:

N(t) Ю P(t) и бN(t)с Ю бP(t)с.

Практически все то же справедливо и для внутренней энергии газа, только процессы, приводящие к случайным изменениям данной суммы другие. Например, подлетая к стенке сосуда, молекула газа сталкивается не с абстрактной абсолютно упруго и зеркально отражающей стенкой, а с одной из частиц, составляющих материал этой стенки. Пусть стенка стальная, тогда это ионы железа, колеблющиеся около положений равновесия – узлов кристаллической решетки. Если молекула газа подлетает к стенке на той фазе колебаний иона, когда он движется ей навстречу, то в результате соударения молекула отлетит от стенки со скоростью большей чем подлетала. Вместе с энергией этой молекулы увеличится и внутренняя энергия газа E. Если молекула сталкивается с ионом, движущемся в том же направлении, что и она, то отлетит эта молекула со скоростью меньшей, чем та, с которой она полетала. Наконец, молекула может попасть в междуузелье (пустое место между соседними узлами кристаллической решетки) и застрять там, так, что даже сильным нагревом ее не извлечь оттуда. В последних двух случаях внутренняя энергия газа E уменьшится. Следовательно, E(t) – также случайная функция времени и – среднее значение этой функции.

Броуновское движение.

Определив положение броуновской частицы в некоторый момент времени t1, можно точно предсказать только то, что ее положение в последующий момент времени t2 не превышает (t2 – t1)·c, где c – скорость света в вакууме.

Различают случаи дискретного и непрерывного спектра состояний и, соответственно, переменной x. Под спектром значений некоторой переменной понимается вся совокупность возможных ее значений.

В случае дискретного спектра состояний для задания распределения вероятностей нужно, во-первых, указать полный набор возможных значений случайной переменной

x1, x2, x3,… xk,… (1)

и, во-вторых, их вероятности:

W1, W2, W3,… Wk,… (2)

Сумма вероятностей всех возможных событий должна быть равна единице (условие нормировки)

(3)

Описание распределения вероятностей соотношениями (1) – (3) невозможно в случае непрерывного спектра состояний и, соответственно, непрерывного спектра возможных значений переменной x. Пусть x принимает все возможные действительные значения в интервале

x О [a, b] (4)

где a и b необязательно конечны. Например, для модуля вектора скорости молекулы газа V О [0, Ґ), а для проекции вектора скорости на направление, скажем, оси OZ: V_zО (–Ґ, +Ґ)¹ (рассматривается случай нерелятивистской теории, когда скорости частиц не ограничены сверху скоростью движения света в вакууме С).

Пусть есть событие (результат измерения x) – значение переменной x принадлежит интервалу [x, x + Dx], лежащему внутри всего интервала возможных значений, т.е. x О [x, x + Dx] О [a, b] (5)

Тогда вероятность DW(x, Dx) попадания x в интервал (5) равна

(6)

Здесь N – полное число измерений x, а Dn(x, Dx) – число результатов, попавших в интервал (5).

Вероятность DW естественно зависит от двух аргументов: x – положения интервала внутри [a, b] и Dx – его длины (предполагается, хотя это совершенно необязательно, что Dx > 0). Например, вероятность получения точного значения x, другими словами, вероятность попадания x в интервал нулевой длины есть вероятность невозможного события и потому равна нулю: DW(x, 0) = 0

С другой стороны, вероятность получить значение x где-то (все равно где) внутри всего интервала [a, b] есть вероятность достоверного события (уж что-нибудь всегда получается) и потому равна единице (принимается, что b > a): DW(a, b – a) = 1.

Пусть Dx мало. Критерий достаточной малости зависит от конкретных свойств системы, которую описывает распределение вероятностей DW(x, Dx). Если Dx мало, то функцию DW(x, Dx) можно разложить в ряд по степеням Dx:

(7)

Если нарисовать график зависимости DW(x, Dx) от второго аргумента Dx, то замена точной зависимости приближенным выражением (7) означает замену (на небольшом участке) точной кривой куском параболы (7).

В (7) первое слагаемое равно нулю точно, третье и последующие слагаемые при достаточной малости Dx можно опустить. Введение обозначения

дает важный результат DW(x, Dx) » r(x)·Dx (8)

Соотношение (8), выполняемое тем точнее, чем меньше Dx означает, что при малой длине интервала, вероятность попадания в этот интервал пропорциональна его длине.

Можно еще перейти от малого, но конечного Dx к формально бесконечно малому dx, с одновременной заменой DW(x, Dx) на dW(x). Тогда приближенное равенство (8) превращается в точное dW(x) = r(x)·dx (9)

Коэффициент пропорциональности r(x) имеет простой смысл. Как видно из (8) и (9), r(x) численно равно вероятности попадания x в интервал единичной длины. Поэтому одно из названий функции r(x) – плотность распределения вероятностей для переменной x.

Функция r(x) содержит в себе всю информацию о том, как вероятность dW(x) попадания x в интервал заданной длины dx зависит от местоположения этого интервала, т.е. она показывает, как вероятность распределена по x. Поэтому функцию r(x) принято называть функцией распределения для переменной x и, тем самым, функцией распределения для той физической системы, ради описания спектра состояний которой была введена переменная x. Термины «плотность распределения вероятностей» и «функция распределения» в статистической физике используются как эквивалентные.

Можно рассмотреть обобщение определения вероятности (6) и функции распределения (9) на случай, к примеру, трех переменных. Обобщение на случай произвольно большого числа переменных выполняется точно также.

Пусть случайно меняющееся во времени состояние физической системы определяется значениями трех переменных x, y и z с непрерывным спектром:

x О [a, b]

y О [c, d]

z О [e, f] (10)

где a, b,…, f, как и ранее, не обязательно конечны. Переменные x, y и z могут быть, например, координатами центра масс молекулы газа, компонентами вектора ее скорости x Ю V_x, y Ю V_y и z Ю V_z или импульса и т.д. Под событием понимается одновременное попадание всех трех переменных в интервалы длины Dx, Dy и Dz соответственно, т.е.:

x О [x, x + Dx]

y О [y, y + Dy]

z О [z, z + Dz] (11)

Вероятность события (11) можно определить аналогично (6)

(12)

с тем отличием, что теперь Dn – число измерений x, y и z, результаты которых одновременно удовлетворяют соотношениям (11). Использование разложения в ряд, аналогичного (7), дает

dW(x, y, z) = r(x, y, z)·dx dy dz (13)

где r(x, y, z) – функция распределения сразу для трех переменных x, y и z.

В математической теории вероятностей термин «функция распределения» используется для обозначения величины отличающейся от r(x), а именно: пусть x – некоторое значение случайной переменной x. Функция Ф(x), дающая вероятность того, что x примет значение не большее, чем x и называется функцией распределения. Функции r и Ф имеют разный смысл, но они связаны между собой. Использование теоремы сложения вероятностей дает (здесь а – левый конец интервала возможных значений x (см. ВЕРОЯТНОСТЕЙ ТЕОРИЯ): , (14) откуда

(15)

Вероятность попадания в интервал произвольной длины [x, x + Dx] можно записать как

(16)

Использование приближенного соотношения (8) дает DW(x, Dx) » r(x)·Dx.

Сравнение с точным выражением (15) показывает, что использование (8) эквивалентно замене интеграла, входящего в (16), произведением подынтегральной функции r(x) на длину промежутка интегрирования Dx:

(17)

Соотношение (17) будет точным, если r = const, следовательно, ошибка при замене (16) на (17) будет невелика, когда подынтегральная функция слабо меняется на длине промежутка интегрирования Dx.

Можно ввести Dx_эфф – длину интервала, на котором функция распределения r(x) меняется существенно, т.е. на величину порядка самой функции, или величина Drэфф по модулю порядка r. Используя формулу Лагранжа, можно написать:

, (18)

откуда следует, что Dx_эфф для любой функции r

(19)

Функцию распределения можно считать «почти постоянной» на некотором промежутке изменения аргумента, если ее приращение |Dr| на этом промежутке по модулю много меньше самой функции в точках этого промежутка. Требование |Dr| << |Drэфф| ~ r (функция распределения r і 0) дает

Dx << Dx_эфф (20)

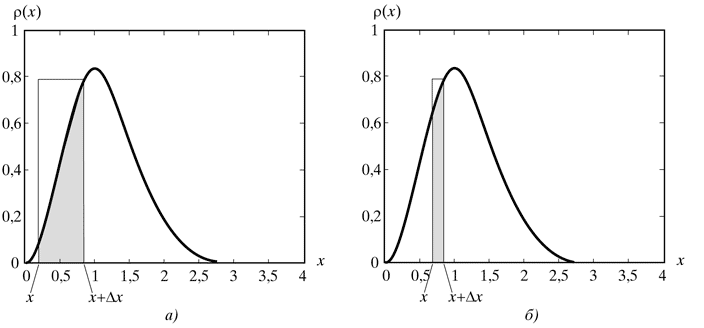
длина промежутка интегрирования должна быть мала по сравнению с той, на которой подынтегральная функция меняется существенно. Иллюстрацией служит рис. 1.

Интеграл в левой части (17) равен площади под кривой. Произведение в правой части (17) – площадь заштрихованного на рис. 1 столбика. Критерием малости отличия соответствующих площадей является выполнение неравенства (20). В этом можно убедиться, подставляя в интеграл (17) первые члены разложения функции r(x) в ряд по степеням

(21)

Требование малости поправки (второго слагаемого в правой части (21) по сравнению с первым и дает неравенство (20) с Dx_эфф из (19).

Примеры ряда функций распределения, играющих важную роль в статистической физике.

Распределение Максвелла для проекции вектора скорости молекулы на заданное направление (для примера, это направление оси OX).

(22)

Здесь m – масса молекулы газа, T – его температура, k – постоянная Больцмана.

Распределение Максвелла для модуля вектора скорости:

(23)

Распределение Максвелла для энергии поступательного движения молекул e = mV2/2

(24)

Распределение Больцмана, точнее, так называемая барометрическая формула, которая определяет распределение концентрации молекул или давления воздуха по высоте h от некоторого «нулевого уровня» в предположении, что температура воздуха от высоты не зависит (модель изотермической атмосферы). В действительности температура в нижних слоях атмосферы заметно падает с ростом высоты.

(25)

Здесь g – ускорение свободного падения.

Зависимости (22) – (25) показаны на рис. 2–5.

, где .

Увеличение a означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа.

При произвольном физическом (или совсем нефизическом) смысле переменных V_x = x – x0 и распределение принято называть распределением Гаусса или нормальным распределением. Распределение Гаусса широко применяется в самых различных областях науки, техники, промышленности и т.п. В последней формуле x0 – наиболее вероятное значение переменной x. Ввиду четности функции относительно разности x – x0 величина x0 совпадает со средним значением переменной x. Параметр s называется дисперсией и характеризует ширину (и высоту) максимума кривой распределения. Чем меньше дисперсия s, тем уже и выше максимум кривой распределения (рис. 2). Если под x понимать такие характеристики человеческого организма как рост, вес, способность к интеллектуальной деятельности (которую удается приближенно измерить с помощью различных тестов) и т.п., то кривые на рис. 2 качественно показывают различие биологических ролей мужчин и женщин. Высокая и узкая (относительно малая дисперсия) пунктирная кривая на рис. 2 – женская, широкая и низкая (относительно большая дисперсия) сплошная кривая на том же рисунке – мужская. Видно, что в среднем женщины заметно совершеннее мужчин. Биологическая задача женщины – сохранить в своих генах оптимальные в данной обстановке качества и передать их потомству. Задача мужчины – определить эти качества.

, где .

Увеличение a означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа.

, где .

Увеличение a означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа.

p(h) = p0·exp(–g·h), где .

Увеличение g означает увеличение массы молекул газа или уменьшение (во столько же раз) температуры газа, p0 – давление на уровне h = 0, переход к формуле (25) осуществляется с помощью уравнения состояния идеального газа p = nkT.

Приведенные выше статистические распределения могут быть получены как частные случаи из наиболее общего большого канонического распределения Гиббса, которое (опять таки как частные случаи) содержит в себе квантовые распределения а) Ферми – Дирака для идеального газа фермионов – частиц с полуцелым спином и 2) Бозе – Эйнштейна для идеального бозонов – частиц с целым спином.

Валериан Гервидс