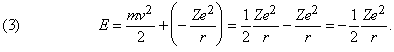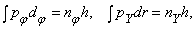АТОМА СТРОЕНИЕ
АТОМА СТРОЕНИЕ, раздел физики, изучающий внутреннее устройство атомов. Атомы, первоначально считавшиеся неделимыми, представляют собой сложные системы. Они имеют массивное ядро, состоящее из протонов и нейтронов, вокруг которого в пустом пространстве движутся электроны. Атомы очень малы – их размеры порядка 10–10–10–9 м, а размеры ядра еще примерно в 100 000 раз меньше (10–15–10–14 м). Поэтому атомы можно «увидеть» только косвенным путем, на изображении с очень большим увеличением (например, с помощью автоэлектронного проектора). Но и в этом случае атомы не удается рассмотреть в деталях. Наши знания об их внутреннем устройстве основаны на огромном количестве экспериментальных данных, которые косвенно, но убедительно свидетельствуют в пользу сказанного выше.
Представления о строении атома радикально изменились в 20 в. под влиянием новых теоретических идей и экспериментальных данных. В описании внутреннего строения атомного ядра до сих пор остаются нерешенные вопросы, которые служат предметом интенсивных исследований. В следующих разделах излагается история развития представлений о строении атома как целого; строению ядра посвящена отдельная статья (АТОМНОГО ЯДРА СТРОЕНИЕ), поскольку эти представления развивались в значительной степени независимо. Энергия, необходимая для исследования внешних оболочек атома, относительно невелика, порядка тепловой или химической энергии. По этой причине электроны были экспериментально обнаружены задолго до открытия ядра.
Ядро же при его малых размерах очень сильно связано, так что разрушить и исследовать его можно только с помощью сил, в миллионы раз более интенсивных, нежели силы, действующие между атомами. Быстрый прогресс в понимании внутренней структуры ядра начался лишь с появлением ускорителей частиц. Именно это огромное различие размеров и энергии связи позволяет рассматривать структуру атома в целом отдельно от структуры ядра.
Чтобы составить представление о размерах атома и незаполненности занимаемого им пространства, рассмотрим атомы, составляющие каплю воды диаметром 1 мм. Если мысленно увеличить эту каплю до размеров Земли, то атомы водорода и кислорода, входящие в молекулу воды, будут иметь в поперечнике 1–2 м. Основная же часть массы каждого атома сосредоточена в его ядре, поперечник которого при этом составил всего 0,01 мм.
АТОМ КАК ЦЕЛОЕ
Историю возникновения самых общих представлений об атоме обычно ведут со времен греческого философа Демокрита (ок. 460 – ок. 370 до н. э.), много размышлявшего о наименьших частицах, на которые можно было бы поделить любое вещество. Группу греческих философов, придерживавшихся того взгляда, что существуют подобные крошечные неделимые частицы, называли атомистами. Греческий философ Эпикур (ок. 342–270 до н.э.) принял атомную теорию, и в первом веке до н.э. один из его последователей, римский поэт и философ Лукреций Кар, изложил учение Эпикура в поэме «О природе вещей», благодаря которой оно и сохранилось для следующих поколений. Аристотель (384–322 до н.э.), один из крупнейших ученых древности, атомистическую теорию не принимал, и его взгляды на философию и науку преобладали впоследствии в средневековом мышлении. Атомистической теории как бы не существовало до самого конца эпохи Возрождения, когда на смену чисто умозрительным философским рассуждениям пришел эксперимент.
В эпоху Возрождения начались систематические исследования в областях, именуемых ныне химией и физикой, принесшие с собой новые догадки о природе «неделимых частиц». Р.Бойль (1627–1691) и И.Ньютон (1643–1727) исходили в своих рассуждениях из представления о существовании неделимых частиц вещества. Однако ни Бойлю, ни Ньютону не потребовалось детальной атомистической теории для объяснения интересовавших их явлений, и результаты проведенных ими экспериментов не сказали ничего нового о свойствах «атомов».
Законы Дальтона.
Первым действительно научным обоснованием атомистической теории, убедительно продемонстрировавшим рациональность и простоту гипотезы о том, что всякий химический элемент состоит из мельчайших частиц, явилась работа английского школьного учителя математики Дж.Дальтона (1766–1844), статья которого, посвященная этой проблеме, появилась в 1803.
Дальтон изучал свойства газов, в частности отношения объемов газов, вступавших в реакцию образования химического соединения, например, при образовании воды из водорода и кислорода. Он установил, что отношения прореагировавших количеств водорода и кислорода всегда представляют собой отношения небольших целых чисел. Так, при образовании воды (H2O) в реакцию с 16 г кислорода вступают 2,016 г газообразного водорода, а при образовании пероксида водорода (H2O2) с 2,016 г водорода соединяются 32 г газообразного кислорода. Массы кислорода, реагирующие с одной и той же массой водорода при образовании этих двух соединений, соотносятся между собой как небольшие числа:
16:32 = 1:2.
На основе подобных результатов Дальтон сформулировал свой «закон кратных отношений». Согласно этому закону, если два элемента соединяются в разных пропорциях, образуя разные соединения, то массы одного из элементов, соединяющиеся с одним и тем же количеством второго элемента, соотносятся как небольшие целые числа. По второму закону Дальтона, «закону постоянных отношений», в любом химическом соединении соотношение масс входящих в него элементов всегда одно и то же. Большое количество экспериментальных данных, относящихся не только к газам, но также и к жидкостям и твердым соединениям, собрал Й.Берцелиус (1779–1848), который провел точные измерения реагирующих масс элементов для многих соединений. Его данные подтвердили сформулированные Дальтоном законы и убедительно продемонстрировали наличие у каждого элемента наименьшей единицы массы.
Атомные постулаты Дальтона имели то преимущество перед абстрактными рассуждениями древнегреческих атомистов, что его законы позволяли объяснить и увязать между собой результаты реальных опытов, а также предсказать результаты новых экспериментов. Он постулировал, что 1) все атомы одного и того же элемента тождественны во всех отношениях, в частности, одинаковы их массы; 2) атомы разных элементов имеют неодинаковые свойства, в частности, неодинаковы их массы; 3) в соединение, в отличие от элемента, входит определенное целое число атомов каждого из составляющих его элементов; 4) в химических реакциях может происходить перераспределение атомов, но ни один атом не разрушается и не создается вновь. (В действительности, как выяснилось в начале 20 в., эти постулаты не вполне строго выполняются, т.к. атомы одного и того же элемента могут иметь разные массы, например водород имеет три такие разновидности, называемые изотопами; кроме того, атомы могут претерпевать радиоактивные превращения и даже полностью разрушиться, но не в химических реакциях, рассматривавшихся Дальтоном.) Основанная на этих четырех постулатах атомная теория Дальтона давала самое простое объяснение законов постоянных и кратных отношений.
Хотя законы Дальтона лежат в основе всей химии, ими не определяются фактические размеры и массы атомов. Они ничего не говорят о числе атомов, содержащихся в определенной массе элемента или соединения. Молекулы простых веществ слишком малы, чтобы их можно было взвесить по отдельности, поэтому для определения масс атомов и молекул приходится прибегать к косвенным методам.
Число Авогадро.
В 1811 А.Авогадро (1776–1856) выдвинул гипотезу, которая значительно упрощала анализ того, как из элементов образуются соединения, и устанавливала различие между атомами и молекулами. Его мысль состояла в том, что равные объемы газов, находящиеся при одинаковых температуре и давлении, содержат одно и то же число молекул. В принципе намек на это можно найти в более ранней работе Ж.Гей-Люссака (1778–1850), который установил, что отношение объемов газообразных элементов, вступающих в химическую реакцию, выражается целыми числами, хотя и отличными от отношений масс, полученных Дальтоном. Например, 2 л газообразного водорода (молекулы H2), соединяясь с 1 л газообразного кислорода (молекулы O2), образуют 1 л паров воды (молекулы H2O).
Истинное число молекул в данном объеме газа чрезвычайно велико, и до 1865 его не удавалось определить с приемлемой точностью. Однако уже во времена Авогадро проводились грубые оценки на основе кинетической теории газов. Очень удобной единицей измерения количества вещества является моль, т.е. количество вещества, в котором столько же молекул, сколько атомов в 0,012 кг самого распространенного изотопа углерода 12С. Один моль идеального газа при нормальных условиях (н.у.), т.е. стандартных температуре и давлении, занимает объем 22,4 л. Число Авогадро – это полное число молекул в одном моле вещества или в 22,4 л газа при н.у. Другие методы, такие, как рентгенография, дают для числа Авогадро N0 более точные значения, нежели полученные на основе кинетической теории. Значение, принятое в настоящее время, таково: 6,0221367Ч1023 атомов (молекул) в одном моле. Следовательно, в 1 л воздуха содержится примерно 3Ч1022 молекул кислорода, азота и других газов.
Важная роль числа Авогадро для физики атома связана с тем, что оно позволяет определить массу и приблизительные размеры атома или молекулы. Поскольку масса 22,4 л газообразного H2 составляет 2,016Ч10–3 кг, масса одного атома водорода равна 1,67Ч10–27 кг. Если считать, что в твердом теле атомы расположены вплотную друг к другу, то число Авогадро позволит приближенно оценить радиус r, скажем, атомов алюминия. Для алюминия 1 моль равен 0,027 кг, а плотность – 2,7Ч103 кг/м3. При этом имеем
откуда r » 1,6Ч10–10 м. Так первые оценки числа Авогадро дали представление об атомных размерах.
Открытие электрона.
Экспериментальные данные, связанные с образованием химических соединений, подтверждали существование «атомных» частиц и позволили судить о малых размерах и массе отдельных атомов. Однако реальная структура атомов, в том числе и существование еще меньших частиц, составляющих атомы, оставалась неясной до открытия Дж.Дж.Томсоном электрона в 1897. До той поры атом считался неделимым и различие в химических свойствах различных элементов не имело своего объяснения. Еще до открытия Томсона был выполнен ряд интересных экспериментов, в которых другие исследователи изучали электрический ток в стеклянных трубках, наполненных газом при низких давлениях. Такие трубки, названные трубками Гейсслера по имени немецкого стеклодува Г.Гейсслера (1815–1879), который первым начал изготовлять их, испускали яркое свечение, будучи подключены к высоковольтной обмотке индукционной катушки. Этими электрическими разрядами заинтересовался У.Крукс (1832–1919), который установил, что характер разряда в трубке меняется в зависимости от давления, и разряд полностью исчезает при высоком вакууме. Более поздние исследования Ж.Перрена (1870–1942) показали, что вызывающие свечение «катодные лучи» представляют собой отрицательно заряженные частицы, которые движутся прямолинейно, но могут отклоняться магнитным полем. Однако заряд и масса частиц оставались неизвестны и было неясно, одинаковы ли все отрицательные частицы.
Огромной заслугой Томсона явилось доказательство того, что все частицы, образующие катодные лучи, тождественны друг другу и входят в состав вещества. С помощью разрядной трубки особого типа, изображенной на рис. 1, Томсон измерил скорость и отношение заряда к массе частиц катодных лучей, позднее названных электронами. Электроны вылетали из катода под действием высоковольтного разряда в трубке. Через диафрагмы D и E проходили только те из них, что летели вдоль оси трубки.
В нормальном режиме эти электроны попадали в центр люминесцентного экрана. (Трубка Томсона была первой «электронно-лучевой трубкой» с экраном, предшественницей телевизионного кинескопа.) В трубке находилась также пара пластин электрического конденсатора, которые, если на них подавалось напряжение, могли отклонять электроны. Электрическая сила FE, действующая на заряд e со стороны электрического поля E, дается выражением
FE = eE.
Кроме того, в той же области трубки с помощью пары катушек с током могло создаваться магнитное поле, способное отклонять электроны в противоположном направлении. Сила FH, действующая со стороны магнитного поля H, пропорциональна напряженности поля, скорости частицы v и ее заряду e:
FH = Hev.
Томсон отрегулировал электрическое и магнитное поля так, чтобы полное отклонение электронов было равно нулю, т.е. электронный пучок вернулся в первоначальное положение. Поскольку в этом случае обе силы FE и FHравны, скорость электронов дается выражением
v = E/H.
Томсон установил, что эта скорость зависит от напряжения на трубке V и что кинетическая энергия электронов mv2/2 прямо пропорциональна этому напряжению, т.е. mv2/2 = eV. (Отсюда термин «электрон-вольт» для энергии, приобретаемой частицей с зарядом, равным заряду электрона при ускорении разностью потенциалов 1 В.) Комбинируя это уравнение с выражением для скорости электрона, он нашел отношение заряда к массе:
Эти опыты позволили определить отношение e/m для электрона и дали приближенное значение заряда e. Точно величина e была измерена Р.Милликеном, который в своих опытах добивался, чтобы заряженные капельки масла висели в воздухе между пластинами конденсатора. В настоящее время характеристики электрона известны с большой точностью:
Таким образом, масса электрона значительно меньше массы атома водорода:
Эксперименты Томсона показали, что электроны в электрических разрядах могут возникать из любого вещества. Поскольку все электроны одинаковы, элементы должны различаться лишь числом электронов. Кроме того, малая величина массы электронов указывала на то, что масса атома сосредоточена не в них.
Масс-спектрограф Томсона.
Вскоре и оставшуюся часть атома с положительным зарядом удалось наблюдать с помощью той же, хотя и модифицированной, разрядной трубки, позволившей открыть электрон. Уже первые эксперименты с разрядными трубками показали, что если катод с отверстием помещается посередине трубки, то через «канал» в катоде проходят положительно заряженные частицы, вызывая свечение люминесцентного экрана, расположенного в противоположном от анода конце трубки. Эти положительные «каналовые лучи» тоже отклонялись магнитным полем, но в направлении, противоположном электронам.
Томсон решил измерить массу и заряд этих новых лучей, также используя для отклонения частиц электрическое и магнитное поля. Его прибор для изучения положительных лучей, «масс-спектрограф», схематически изображен на рис. 2. Он отличается от прибора, представленного на рис. 1, тем, что электрическое и магнитное поля отклоняют частицы под прямым углом друг к другу, а потому «нулевое» отклонение получить не удается. Положительно заряженные атомы на пути между анодом и катодом могут потерять один или несколько электронов, и по этой причине могут ускоряться до различных энергий. Атомы одного типа с одинаковыми зарядом и массой, но с некоторым разбросом конечных скоростей, вычертят на люминесцентном экране или фотопластинке кривую линию (отрезок параболы). При наличии атомов с различной массой более тяжелые атомы (с тем же зарядом) будут отклоняться от центральной оси слабее, чем более легкие. На рис. 3 приведена фотография парабол, полученных на масс-спектрографе Томсона. Самая узкая парабола соответствует самому тяжелому однократно ионизованному атому (атому ртути), у которого выбит один электрон. Две самые широкие параболы соответствуют водороду, одна – атомарному H+, а другая – молекулярному H2+, причем оба однократно ионизованы. В некоторых случаях теряются два, три и даже четыре заряда, однако атомарный водород никогда не наблюдался ионизованным более чем однократно. Данное обстоятельство было первым указанием на то, что в атоме водорода только один электрон, т.е. это самый простой из атомов.
Другие доказательства сложной структуры атома.
В то самое время, когда Томсон и другие исследователи экспериментировали с катодными лучами, открытие рентгеновского излучения и радиоактивности принесло дополнительные доказательства сложной структуры атома. В 1895 В.Рентген (1845–1923) случайно обнаружил таинственное излучение («Х-лучи»), проникавшее сквозь черную бумагу, которой он оборачивал трубку Крукса при исследовании зеленой люминесцирующей области электрического разряда. Х-лучи вызывали свечение удаленного экрана, покрытого кристаллическим платиноцианидом бария. Рентген выяснил, что различные вещества разной толщины, введенные между экраном и трубкой, ослабляют свечение, но не гасят его полностью. Это свидетельствовало о чрезвычайно высокой проникающей способности Х-лучей. Рентген установил также, что эти лучи распространяются прямолинейно и не отклоняются под действием электрических и магнитных полей. Возникновение такого невидимого проникающего излучения при бомбардировке электронами различных материалов было чем-то совершенно новым. Было известно, что видимый свет от трубок Гейсслера состоит из отдельных «спектральных линий» с определенными длинами волн и, значит, связан с «колебаниями» атомов, имеющими дискретные частоты. Существенная особенность нового излучения, отличавшая его от оптических спектров, помимо высокой проникающей способности, состояла в том, что оптические спектры элементов с последовательно возраставшим числом электронов полностью отличались друг от друга, тогда как спектры X-лучей очень незначительно изменялись от элемента к элементу.
Еще одним открытием, имеющим отношение к строению атома, было то, что атомы некоторых элементов могут спонтанно испускать излучение. Это явление было обнаружено в 1896 А.Беккерелем (1852–1908). Беккерель открыл радиоактивность, используя соли урана в процессе изучения люминесценции солей под действием света и ее связи с люминесценцией стекла в рентгеновской трубке. В одном из опытов наблюдалось почернение фотопластинки, завернутой в черную бумагу и находившейся около урановой соли в полной темноте. Это случайное открытие стимулировало интенсивные поиски других примеров естественной радиоактивности и постановку опытов по определению природы испускаемого излучения. В 1898 П.Кюри (1859–1906) и М.Кюри (1867–1934) обнаружили еще два радиоактивных элемента – полоний и радий. Э.Резерфорд (1871–1937), исследовав проникающую способность излучения урана, показал, что имеются два типа излучений: очень «мягкое» излучение, которое легко поглощается веществом и которое Резерфорд назвал альфа-лучами, и более проникающее излучение, которое он назвал бета-лучами. Бета-лучи оказались тождественными обычным электронам, или «катодным лучам», возникающим в разрядных трубках. Альфа-лучи, как выяснилось, имеют такие же заряд и массу, как и атомы гелия, лишенные двух своих электронов. Третий тип излучения, названный гамма-лучами, оказался сходен с X-лучами, но обладал еще большей проникающей способностью.
Все эти открытия ясно показали, что атом не является «неделимым». Он не только состоит из более мелких частей (электронов и более тяжелых положительных частиц), но эти и другие субчастицы, по-видимому, самопроизвольно испускаются при радиоактивном распаде тяжелых элементов. Кроме того, атомы не только испускают излучение в видимой области с дискретными частотами, но и могут так возбуждаться, что начинают испускать более «жесткое» электромагнитное излучение, а именно X-лучи.
Модель атома Томсона.
Дж.Томсон, внесший огромный вклад в экспериментальное изучение строения атома, стремился найти модель, которая позволила бы объяснить все его известные свойства. Поскольку преобладающая доля массы атома сосредоточена в его положительно заряженной части, он принял, что атом представляет собой сферическое распределение положительного заряда радиусом примерно 10–10 м, а на его поверхности находятся электроны, удерживаемые упругими силами, позволяющими им колебаться (рис. 4). Суммарный отрицательный заряд электронов в точности компенсирует положительный заряд, так что атом электрически нейтрален. Электроны находятся на сфере, но могут совершать простые гармонические колебания относительно положения равновесия. Такие колебания могут происходить лишь с определенными частотами, которым соответствуют узкие спектральные линии, наблюдающиеся в газоразрядных трубках. Электроны можно довольно легко выбить с их позиций, в результате чего возникают положительно заряженные «ионы», из которых состоят «каналовые лучи» в опытах с масс-спектрографом. X-лучи соответствуют очень высоким обертонам основных колебаний электронов. Альфа-частицы, возникающие при радиоактивных превращениях, – это часть положительной сферы, выбитая из нее в результате какого-то энергичного разрывания атома.
Однако эта модель вызывала ряд возражений. Одно из них было связано с тем, что, как обнаружили спектроскописты, измерявшие линии испускания, частоты этих линий не являются простыми кратными низшей частоты, как должно быть в случае периодических колебаний заряда. Вместо этого они сближаются с увеличением частоты, как если бы стремились к пределу. Уже в 1885 И.Бальмеру (1825–1898) удалось найти простую эмпирическую формулу, связывающую частоты линий видимой части спектра водорода:
где n – частота, c – скорость света (3Ч108 м/с), n – целое число и RH – некий постоянный множитель. Согласно этой формуле, в данной серии спектральных линий водорода должны отсутствовать линии с длиной волны l меньше 364,56 нм (или с более высокими частотами), отвечающей n = Ґ. Так оно и оказалось, и это стало серьезным возражением против модели атома Томсона, хотя и делались попытки объяснить расхождение различием упругих возвращающих сил для разных электронов.
Исходя из модели атома Томсона, было также крайне трудно объяснить испускание атомами рентгеновского или гамма-излучения.
Затруднения в модели атома Томсона вызвало и отношение e/m заряда к массе для атомов, потерявших свои электроны («каналовых лучей»). Самый простой атом – атом водорода с одним электроном и сравнительно массивной сферой, несущей один положительный заряд. Значительно раньше, в 1815, У.Праут высказал предположение, что все более тяжелые атомы состоят из атомов водорода, и было бы понятно, если бы масса атома возрастала пропорционально числу электронов. Однако измерения показали, что отношение заряда к массе для разных элементов неодинаково. Например, масса атома неона примерно в 20 раз больше массы атома водорода, тогда как заряд составляет лишь 10 единиц положительного заряда (у атома неона 10 электронов). Дело обстояло так, как если бы положительный заряд имел переменную массу или же электронов было действительно 20, но 10 из них находились внутри сферы.
Опыты Резерфорда по рассеянию.
Затем возникла еще одна трудность. В 1903 Ф.Ленард (1862–1947) ставил опыты с прохождением пучка быстрых электронов сквозь тонкие металлические фольги. В модели атома Томсона почти все пространство заполнено веществом (положительно заряженной частью атома), а потому можно было думать, что сквозь фольгу сможет проникать лишь очень мало электронов. Ленард же обнаружил, что сквозь фольгу проходят почти все электроны. Хотя в эксперименте имелись трудности, связанные с малой массой бомбардирующих частиц, Ленард выдвинул предположение, что масса атома сосредоточена в «динамиде» – его центральной области, значительно меньшей, чем предполагалось.
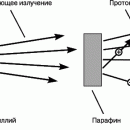
Решающий эксперимент, совершенно изменивший представления о пространственной структуре атома, был проведен Э.Резерфордом и его сотрудниками Х.Гейгером (1882–1945) и Э.Марсденом (1889–1970). Вместо электронов они использовали альфа-частицы, т.к. благодаря своей большей массе (в 7350 раз больше массы электрона) эти частицы не претерпевают заметного отклонения при столкновении с атомными электронами, что позволяет регистрировать только столкновения с положительной частью атома. В качестве источника альфа-частиц был взят радий, а частицы, претерпевавшие рассеяние в тонкой металлической фольге, например золотой, регистрировались по «сцинтилляционным» вспышкам на экране из сульфида цинка, находящемся в затемненной комнате. Схема опыта представлена на рис. 5.
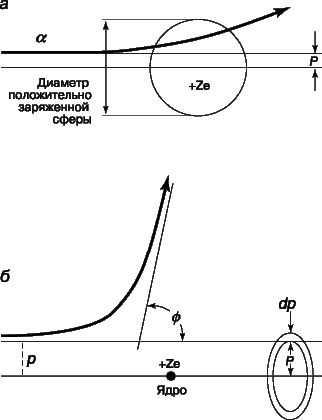
Согласно модели Томсона, практически все альфа-частицы должны оказываться в пределах очень малого угла относительно своего первоначального направления, поскольку большую часть времени они должны были бы проходить в области почти равномерно распределенного положительного заряда. Хотя результаты Резерфорда согласовались с ожидаемым распределением в области малых отклонений, было зарегистрировано очень много отклонений на углы, гораздо большие, чем предсказывала модель атома Томсона. Столь большие отклонения можно было объяснить лишь тем, что положительная «сердцевина» атома значительно меньше размеров его электронной структуры и, следовательно, альфа-частицы могут очень близко подходить к этой малой положительной сердцевине, встречая при этом очень большие кулоновские силы. Опыты Резерфорда убедительно показали, что весь атом, кроме очень малой массивной сердцевины, или «ядра», как и предполагал Ленард, почти полностью пуст. Исходя из полученных им экспериментальных данных, Резерфорд заключил, что диаметр ядра атома золота составляет не более 6Ч10–15 м – значение, довольно близкое к современному.
Резерфорду удалось, упрощенно рассматривая ядро как точечный центр рассеяния, на основе только электростатики и механики Ньютона вывести формулу для углового распределения рассеянных частиц. Между альфа-частицей с массой M и зарядом 2e, где e – заряд электрона, и ядром с зарядом Ze, где Z – атомный номер элемента, из которого состоит рассеивающее вещество, действует сила электростатического отталкивания 2Ze2/r2, где r – расстояние между зарядами. Угол j, на который происходит рассеяние, зависит от параметра столкновения p, т.е. минимального расстояния, на котором частица прошла бы мимо ядра, если бы не отклонилась.
Как видно из рис. 6, наибольшему углу отклонения отвечает наименьший параметр столкновения. Доля альфа-частиц, отклоняющихся на угол j и более, дается выражением
где n – число атомов в 1 см3, t – толщина фольги, M и v – масса и скорость альфа-частицы и Z – заряд ядра. Этот закон рассеяния Резерфорда чаще записывают в виде доли частиц df, которая рассеивается в телесный угол dw в интервале углов от j до j + dj:
Эти выражения получили количественное подтверждение для широкого диапазона углов и разных рассеивающих материалов и позволили измерить заряд ядра.
Резерфордовская, или ядерная, модель атома, вытеснив томсоновскую модель, явилась важным этапом на пути создания квантовой механики. Детальные эксперименты, выполненные Гейгером и Марсденом в 1913, не оставили и тени сомнения в том, что картина атома с малым массивным ядром в центре электронной структуры значительно больших размеров верна не только качественно, но и количественно. Некоторые детали, перенесенные из томсоновской модели, такие, как существование в ядре электронов, позднее также были отброшены.
Квантовая теория Бора.
Н.Бор (1885–1962) работал в 1912–1913 у Резерфорда, когда тот проводил опыты по рассеянию, и вернулся в 1913 в Копенгаген с множеством новых идей. Требовал своего объяснения ряд явлений, помимо только что открытых в «ядерных» экспериментах по рассеянию. Теперь, когда была отвергнута томсоновская модель атома, узкие, дискретные спектральные линии в излучении разрядных трубок и эмпирические закономерности в их частотах казались еще менее понятными.
Был и другой атомный эффект, открытый в 1887 Г.Герцем (1857–1894), а именно фотоэффект. Суть его в том, что свет, падающий на свежеочищенную поверхность металла, выбивает из нее электроны, если частота света достаточно высока. Для каждого металла имеется своя пороговая частота. Опыты показали, что тормозящее электростатическое поле, уменьшающее до нуля ток фотоэлектронов, не зависит от интенсивности света, но зависит от его длины волны. Электромагнитная теория, согласно которой свет представляет собой электромагнитные волны, оказалась не в состоянии объяснить это, поскольку по этой теории для испускания электрона с любой скоростью атому нужно только достаточно долго поглощать энергию. В 1905 А.Эйнштейн (1879–1955) предложил объяснение фотоэффекта, которое полностью согласовалось с экспериментальными данными, но требовало коренного пересмотра существовавшей концепции света как волнового процесса. Эйнштейн предположил, что свет переносит энергию порциями, которые называются фотонами или квантами света, причем их энергия дается выражением E = hn, где n – частота света, а h – «постоянная Планка», равная 6,626Ч10–34 ДжЧс. Попадая на поверхность металла, фотон передает всю свою энергию электрону. Поскольку электрон связан с поверхностью электростатическими силами, ему для вылета необходима энергия W («работа выхода»), а остальная часть полученной электроном энергии превращается в его кинетическую энергию, т.е. hn = W + 1/2mv2. Гипотеза Эйнштейна объясняла, почему кинетическая энергия фотоэлектронов зависит от частоты света, а число испускаемых электронов – от его интенсивности.
Как часто происходит с научными открытиями, оказалось, что гипотеза «квантов» Эйнштейна имеет в своей основе более раннюю теорию. М.Планк (1858–1947) первым привлек идею квантования для объяснения наблюдаемого спектрального состава излучения нагретых тел. Ему удалось объяснить спектр, предположив, что гармонические осцилляторы поглощают и излучают лишь дискретные порции энергии hn.
Бор блестяще применил квантовую гипотезу к описанию орбит электронов в атомах и их излучения. Он отбросил идею о том, что электроны ведут себя подобно осцилляторам, а вместо этого представил динамику атома в виде движения электронов по орбитам вокруг ядра, наподобие движения планет по орбитам вокруг Солнца. Сила электростатического притяжения электрона ядром является центростремительной силой, заставляющей электрон двигаться по круговой орбите радиуса r со скоростью v. В общем случае ядра с зарядом Ze имеем
В таком силовом поле (когда сила обратно пропорциональна расстоянию до центра притяжения) кинетическая энергия движения всегда равна – 1/2 потенциальной энергии:
а полная энергия, т.е. сумма кинетической и потенциальной энергий, равна:
Эти соотношения следуют из обычных законов механики и электростатики. Бор, в дополнение к ним, сформулировал следующие постулаты, составляющие основу квантовой теории атома.
I. Разрешены только такие круговые орбиты, для которых момент импульса равен целому числу в единицах постоянной Планка, деленной на 2p. (Момент импульса тела l, движущегося по круговой орбите, равен произведению его массы m на скорость v и радиус орбиты r.) Таким образом,
II. Хотя, согласно электромагнитной теории, любая заряженная частица, движущаяся с ускорением, должна испускать излучение, электроны не испускают излучения, двигаясь по своим орбитам внутри атома. Излучение возникает только при переходе электрона с одной квантованной орбиты на другую.
III. Частота этого излучения определяется изменением полной энергии, т.е. разностью энергий атома в начальном и конечном состояниях:
hn = E2 – E1.
Эти условия квантования энергии приводят к дискретным орбитам электронов. Решая уравнение (2) относительно скорости и подставляя в (4), получаем
или, если ввести «боровский радиус» a0 = h2/4p2me2 » 5,29Ч10–11 м,
На рис. 7 изображены первые шесть орбит электронов в атоме водорода, соответствующие теории Бора. Показаны также переходы, сопровождающиеся испусканием дискретных спектральных линий. Каждая серия спектральных линий носит имя ее открывателя; из всех серий лишь часть серии Бальмера лежит в видимой области спектра.
На рис. 8 показано, как выглядят линии серии Бальмера на фотопластинке спектрографа. Нетрудно видеть, что линии сгущаются вблизи границы серии.
Энергии состояний атома, отвечающих каждому целому значению n, также квантованы:
Используя третий постулат Бора и соотношение с = ln между скоростью, длиной волны и частотой, можно теперь объяснить эмпирическую формулу, найденную Бальмером для его серии линий:
просто как частный случай формулы Бора. С ее помощью можно вычислить «постоянную Ридберга» RH :
Значение RH, найденное Бальмером, составляло 10967776 м–1; используя имевшиеся в то время значения m, e, c и h, Бор получил RH = 1,03Ч107 м–1. Современное значение RH составляет 10979708 м–1. Таким образом, соответствие теории Бора с экспериментом достаточно хорошее. Расхождение в величине RH объясняется неточностью значений фундаментальных констант m, e, c, h, которыми пользовался Бор, а также необходимостью учета ряда поправок, главной из которых является поправка на движение ядра (см. ниже).
Таким образом, Бор своей теорией с самого начала добился значительного успеха, дав не только качественное, но и количественное объяснение линиям водородного спектра и применив представления Планка и Эйнштейна о квантах в теории оптических спектров.
В 1914 Дж.Франк (1882–1964) и Г.Герц (1887–1975) экспериментально подтвердили правильность представления о квантовании энергетических уровней, бомбардируя атомы паров ртути электронами с известной энергией. Они измеряли энергию, теряемую электронами при рассеянии на атомах ртути. Электроны с энергией ниже определенного порогового значения вообще не передавали энергию атомам ртути; но, как только энергия электронов оказывалась достаточной для возбуждения перехода атома ртути на ближайший уровень с более высокой энергией, электроны интенсивно передавали свою энергию. Это было убедительным доказательством существования квантованных энергетических уровней.
Теория Бора позволила объяснить и происхождение рентгеновского излучения (X-лучей): это излучение испускается в результате выбивания (бомбардирующим атом электроном) электрона с внутренней орбиты атома: на освободившееся место переходят электроны с внешних оболочек атома. Поскольку энергия при этом изменяется значительно больше, чем при оптическом переходе, рентгеновское излучение оказывается более коротковолновым, нежели видимый свет, и более проникающим. Теория Бора объяснила не только линии Бальмера, наблюдаемые в видимой части спектра, но и другие серии линий в ультрафиолетовой (серию Лаймана) и инфракрасной (серию Пашена) области, которые были обнаружены с помощью фотографических методов.
Хотя масса M ядра водорода (протона) значительно больше массы электрона, движущегося по орбите в атоме, было бы неправильным считать, что в этой «динамической» модели атома протон покоится. Как указал А.Зоммерфельд (1868–1951), в силу законов сохранения энергии и импульса ядро и электрон должны вращаться относительно общего центра масс с одинаковой угловой скоростью (при этом ядро расположено гораздо ближе к центру масс). Влияние этого движения ядра на энергию электронных состояний можно учесть, просто заменив массу электрона m «приведенной массой»
где M – масса ядра рассматриваемого атома. В случае водорода величина m меньше m на 1/1837. Однако точность спектроскопических измерений такова, что такая поправка заметно улучшает согласие теории с экспериментом.
Эффектной демонстрацией возможностей модифицированной теории Бора для атома водорода явилось открытие «тяжелого водорода» (дейтерия) 2Н. Масса ядра дейтерия почти вдвое превышает массу протона, и хотя дейтерий составляет всего 1/4500 часть обычного газообразного водорода, его наличие проявляется на фотоснимках спектра, сделанных с высоким разрешением, в виде очень слабых линий, сдвинутых относительно основных линий из-за различия в величине m. После того как Ф.Астон (1977–1945) обнаружил в 1931 очевидное расхождение в значениях атомной массы водорода, Р.Бёрдж (1887–1980) и Д.Менцель выдвинули гипотезу о существовании двух разновидностей водорода с разными массами изотопов. В 1932 Г.Юри (1893–1981), Дж.Мерфи и Ф.Брикведде (1903–1989) провели серию экспериментов, в которых спектр водорода фотографировался с помощью вогнутой дифракционной решетки радиусом 6,4 м. Они обнаружили слабые дейтериевые линии там, где их предсказывали (длина волны, отвечающая линии Ha , была смещена на 179,3 нм), и, взяв образцы, обогащенные тяжелым изотопом, получили не вызывающие сомнения яркие линии.
Зоммерфельд развил далее теорию Бора, указав на то, что круговые орбиты – это лишь частный случай и что постулаты Бора могут быть введены и в случае эллиптических орбит. (При движении по эллиптической орбите скорость наряду с азимутальной имеет и радиальную составляющую. При этом движение происходит в одной плоскости, а центр притяжения располагается в одном из фокусов.) Таким образом, на обобщенный импульс pi налагаются два условия квантования, связанные с «периодическими координатами» qi. (Область изменения периодических координат повторяется с определенным периодом; например, угловое положение электрона относительно ядра представляет собой периодическую координату.) В общем случае
Таким образом, для того чтобы орбита существовала, интеграл от импульса по координате за период должен быть равен целому числу постоянных Планка. При движении по эллиптической орбите существуют два независимых уравнения
где pj – азимутальный, а pr – радиальный импульс. (Радиальный импульс prравен произведению массы на радиальную скорость, которая в случае круговой орбиты равна нулю.) Классическая механика движения по эллиптическим орбитам, справедливая для описания движения планет, была хорошо известна, и, следовательно, ее можно было непосредственно использовать в случае атомных орбит. Согласно механике Ньютона, переход от эллиптической орбиты к круговой не сопровождается изменением энергии уровня, поскольку в случае эллипса энергия зависит только от большой полуоси эллипса, которая в свою очередь зависит лишь от
Таким образом, число n («главное квантовое число») отвечает одной и той же энергии для некоего набора эллиптических орбит, включающего в себя и круговую, для которой nY = 0.
Измерения, проведенные с более высоким разрешением, показали существование «тонкой структуры» спектральных линий (одна широкая «линия» в действительности состоит из нескольких линий). Частично это было связано с тем, как было показано Зоммерфельдом, что электроны движутся со скоростями, сравнимыми со скоростью света и, следовательно, вместо механики Ньютона следует использовать релятивистскую механику Эйнштейна. В результате в энергиях эллиптических орбит возникает небольшое различие, поскольку скорости меняются в зависимости от эсцентриситета. Поправка может быть выражена через квантовые числа n и nj:
где величина
есть так называемая постоянная тонкой структуры, или постоянная Зоммерфельда. Существование этих небольших поправок, зависящих от эллиптичности орбиты, значительно увеличивает число возможных переходов. Чтобы учесть отсутствие некоторых из предсказанных спектральных линий, пришлось ввести «правила отбора», допускающие изменение азимутального квантового числа nj только на +1 или -1.
Таким образом, квантовая теория Бора, дополненная более точной механикой орбитального движения Зоммерфельда, оказалась способной объяснить широкий круг явлений. Стало понятным существование серий спектральных линий водорода, наличие их тонкой структуры, характеристики неупругого рассеяния электронов в газах и изотопическое смещение спектральных линий. Кроме того, удалось точно вычислить потенциал ионизации водорода (энергию, необходимую для выбивания электрона из атома).
Однако трудности все же остались. Теория Бора давала хорошие результаты в случае одноэлектронных атомов типа водорода, однократно ионизованного гелия, дважды ионизованного лития, а также, например, натрия (благодаря тому, что в атоме натрия есть один слабо связанный электрон, котрый в основном и определяет как спектр, так и химические свойства натрия), но она плохо описывала обычный атом гелия с двумя электронами и другие многоэлектронные атомы. Неудачными оказались также попытки Бора объяснить хорошо известные изменения химических и физических свойств при переходе от атома к атому. Наконец, и постулаты Бора, например, квантование момента импульса на электронных орбитах, выглядели совершенно произвольными.
Дело в том, что в то время были неизвестны два положения, без которых понять строение сложных атомов невозможно, – принцип запрета Паули и существование у электрона спина. Эти положения наряду с созданием новой механики, названной волновой, или квантовой, были необходимы для полного понимания строения атома.
Квантовая механика атома.
Недостатки теории Бора, основанной на механике классических частиц с дополнением в виде квантовых постулатов, высветили фундаментальную проблему правильного описания движения электронов на малых расстояниях, например, внутри атома. Опираясь на то, что свет имеет как корпускулярные, так и волновые свойства (в некторых явлениях, например, при фотоэффекте, он ведет себя как поток частиц, а в некоторых, например, при интерференции, как волна), Л.де Бройль (1892–1987) в 1923 выдвинул гипотезу о том, что корпускулярно-волновой дуализм свойствен также и веществу. Поскольку квантовая теория приписывает световым фотонам при фотоэффекте корпускулярное поведение, можно допустить, что электроны в атомах могут вести себя на своих «орбитах» подобно волнам. Де Бройль пришел к выводу, что с движением любого вида частиц можно «ассоциировать» распространение волны, если приписать частице с массой m и скоростью v длину волны
l = h/mv.
Экспериментальным подтверждением волновых свойств частиц явилось открытое в 1927 К.Дэвиссоном (1881–1958) и Л.Джермером (1896–1971) явление дифракции электронов. Угловое распределение электронов при отражении пучка электронов от поверхности кристалла можно объяснить лишь на основе волновых представлений, причем наблюдалось согласие с постулированным де Бройлем соотношением между длиной волны и скоростью.
Разработка квантовой механики В.Гейзенбергом (1901–1976), Э.Шрёдингером (1887–1961) и другими теоретиками в период, последовавший за высказанной де Бройлем гипотезой, привела к прояснению ситуации с теорией Бора. Например, в теории Бора условие «стационарных состояний»
mvЧ2pr = nh
носило характер произвольного требования. Теперь же оно выступает как требование, чтобы на периодической орбите электрона укладывалось целое число длин волн де Бройля. Разрешенными оказываются именно те орбиты, которые удовлетворяют этому требованию.
При решении волнового уравнения Шрёдингера для атома водорода естественным образом возникают три квантовых числа, обычно обозначаемые символами n, l и ml. Здесь n – целое число, принимающее любые значения, большие 0, которое называется главным квантовым числом электрона. Оно соответствует числу n, обозначавшему различные боровские орбиты. Число l (орбитальное квантовое число) тоже целое и может принимать любые значения от 0 до (n – 1). Оно характеризует орбитальный момент импульса электрона и тесно связано с nj в модели Бора. Из решения волнового уравнения следует, что разрешены только значения орбитального момента импульса электрона, равные:
При 
максимально допустимое значение l равно нулю, и, следовательно, орбитальный момент импульса электрона тоже должен быть равен нулю.
Третье квантовое число ml называется «магнитным квантовым числом» и играет важную роль, когда атом находится в магнитном поле H. В этом случае квантуется не только орбитальный момент импульса pj, но и его проекция на направление магнитного поля. Проекция квантового числа l на направление поля H также должна быть целым числом, ml. Таким образом, ml может принимать (2l + 1) значений: +l, (l – 1), (l – 2),..., –(l – 1), –l. В рамках модели Бора это соответствует заданию угла q наклона плоскости электронной орбиты относительно направления магнитного поля, как показано на рис. 9:
cosq = ml/l.
Если l = 3, то существует (2l + 1), т.е. 7 различных дискретных значений угла, которые могут составлять боровские орбиты с направлением H (рис. 9,б).
Еще одно следствие правил квантования ml состоит в том, что магнитный момент m может принимать значения
m = leh/4pmc = lm,
где величина m0, так называемый магнетон Бора, равна 9,27Ч10–24 Дж/Тл. Изменение энергии электрона, обусловленное взаимодействием его момента с магнитным полем, равно:
DE = m0Hml.
Таким образом, магнитное поле приводит к расщеплению уровней и увеличению числа переходов и спектральных линий, т.е. к эффекту Зеемана.
Спин электрона и принцип запрета Паули.
В то время, когда формировались идеи квантовой механики, для объяснения характеристик линейчатых спектров атомов была выдвинута гипотеза спина электрона. Спектроскопия более высокого разрешения показала, что многие линии представляют собой дублеты, которые не удается объяснить, исходя из орбитального движения электронов. Особенно показательный пример – дублет желтых линий натрия 589,0 и 589,6 нм, который четко разделяется даже простыми спектрометрическими приборами.
Для объяснения частого появления дублетов в линейчатых спектрах Дж.Уленбек (1900–1988) и С.Гаудсмит (1902–1978) выдвинули в 1925 предположение, что электрон имеет собственный момент импульса, или спин, т.е. его можно представить себе вращающимся вокруг собственной оси одновременно с вращением по орбите вокруг ядра, аналогично вращению Земли при ее движении вокруг Солнца. Спин характеризуется еще одним квантовым числом, s. Поскольку вектор спинового момента импульса имеет (2s + 1) различных ориентаций, а наблюдаемая кратность энергетических уровней равна двум, имеем (2s + 1) = 2, или s = 1/2. Проекции вектора s на некое выделенное направление (направление внешнего магнитного поля) характеризуются спиновым магнитным квантовым числом ms, которое может быть равно либо +1/2, либо -1/2. Вращающийся вокруг собственной оси электрон подобен крошечному магниту с магнитным моментом
В конечном итоге получается 4 независимых квантовых числа, характеризующих состояние электрона в атоме:
n – главное квантовое число;
l – орбитальное квантовое число;
ml – орбитальное магнитное квантовое число;
ms – спиновое магнитное квантовое число.
Хотя квантовая механика позволяет, если заданы квантовые числа, определить энергию состояния и пространственное распределение электронной плотности вероятностей (заменяющее орбиты в модели Бора), для фиксации числа электронов в каждом состоянии требуются дальнейшие предположения.
В 1925 В.Паули (1900–1958) сформулировал «принцип запрета», который сразу внес ясность в очень многие атомные явления. Он предложил простое правило: в каждом отдельном квантовом состоянии может находиться только один электрон. Это означает, что набор чисел, отвечающих данным n, l и ml, зависит от n. Например, при n = 1 возможно лишь l = 0; следовательно, ml = 0 и единственное различие состояний связано с ms = +1/2 и -1/2. В таблице приведены возможности, отвечающие различным n. Отметим, что в первой «оболочке» (n = 1) имеются 2 электрона, в следующей оболочке (n = 2) имеется 8 электронов, образующих две подоболочки, и т.д. Максимальное число электронов в подоболочке равно 2(2l + 1), а максимальное число подоболочек составляет n. Для каждого n полностью заполненная оболочка содержит 2n2 электронов.
| ВОЗМОЖНОЕ ЧИСЛО ЭЛЕКТРОНОВ В ДАННОЙ ОБОЛОЧКЕ | |||||
| n | l | ml | ms | Число электронов в подоболочке | Число электронов в заполненной оболочке |
| 1 1 |
0 0 |
0 0 |
+1/2 –1/2 |
2 | 2 |
| 2 2 |
0 0 |
0 0 |
+1/2 –1/2 |
2 | |
| 2 2 2 2 2 2 |
1 1 1 1 1 1 |
–1 –1 0 0 1 1 |
+1/2 –1/2 +1/2 –1/2 +1/2 –1/2 |
6 | 8 |
| 3 3 |
0 0 |
0 0 |
+1/2 –1/2 |
2 | |
| 3 3 3 3 3 3 |
1 1 1 1 1 1 |
–1 –1 0 0 1 1 |
+1/2 –1/2 +1/2 –1/2 +1/2 –1/2 |
6 | |
| 3 3 3 3 3 3 3 3 3 3 |
2 2 2 2 2 2 2 2 2 2 |
–2 –2 –1 –1 0 0 1 1 2 2 |
+1/2 –1/2 +1/2 –1/2 +1/2 –1/2 +1/2 –1/2 +1/2 –1/2 |
10 | 18 |
Соответствие принципа Паули эксперименту было подтверждено огромным числом спектроскопических наблюдений, а также многочисленными данными электронной теории металлов, физики ядерных процессов, низкотемпературных явлений. Это один из наиболее фундаментальных объединяющих принципов физики, открывший путь к пониманию электронной структуры сложных атомов. Правда, принципом Паули определяется лишь возможность заполнения различных электронных оболочек, а для проверки фактического заполнения тех или иных состояний необходимы данные, полученные на основе оптических и рентгеновских спектров. Но в атомах вплоть до аргона с Z = 18 каждый дополнительный электрон просто добавляется в низшую из незаполненных подоболочек. Отступления от этого порядка наблюдаются у более сложных атомов, оболочки которых частично перекрываются. Квантовая механика объясняет это отступление тем, что в первую очередь заполняются состояния с самой низкой энергией.
Детальный анализ электронной структуры и распределения электронов с точки зрения квантовой механики и принципа Паули в более тяжелых атомах весьма сложен. Для состояния 1s (n = 1, l = 0) возможно только сферически симметричное распределение (причем наиболее вероятным оказывается положение электрона в центре атома). В состоянии 2p (n = 2, l = 1) момент импульса электрона уже не равен нулю, и поэтому масимум плотности находится на ненулевом расстоянии от ядра. Распределение электронной плотности зависит от квантового числа ml в соответствии с требованием квантования компонент момента импульса вдоль направления магнитного поля.
Периодическая система элементов.
Число электронов, находящихся в оболочках нейтрального атома, равное числу протонов в его ядре, называется атомным номером элемента. Периодическая система элементов, предложенная в 1869 Д.И.Менделеевым (1834–1907) – это таблица, в которой элементы располагаются в порядке возрастания атомного номера и распределяются по периодам так, что атомы со сходными химическими свойствами попадают в одну и ту же группу. Например, группа, содержащая гелий, неон, аргон, криптон, ксенон и радон, составляет группу инертных газов; это атомы с заполненными электронными оболочками, а из заполненной оболочки почти так же трудно удалить электрон, как и добавить в нее лишний. Кроме того, эти газы – одноатомные, их молекулы представляют собой один атом (см. также ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ).
Химические свойства атомов в значительной степени определяются внешними электронами. Простой характер таблицы вплоть до аргона (атомный номер которого Z = 18) обусловлен тем, что при добавлении очередного электрона вплоть до Z = 18 последовательно заполняется низшая подоболочка. Значительное же усложнение таблицы после Z = 18 объясняется усложнением последовательности заполнения подоболочек. Для случая, когда имеется большое число электронов, точные решения уравнений квантовой механики получить не удается, и используются приближенные методы. Одно из приближений состоит в том, что атом с единственным электроном сверх заполненной оболочки, такой, как натрий, Z = 11, рассматривается как «одноэлектронный» атом. И действительно, упрощенная теория Бора (модифицированная с учетом значения n = 3 для состояния электрона) дает довольно точные значения для энергии уровней (но не для расщепления линий).
Дальнейшее исследование структуры атомов.
В настоящее время электронная структура атомов в принципе получила свое объяснение, хотя свойства многоэлектронных атомов удается рассчитать лишь приближенно. Квантовая механика объясняет все известные свойства отдельных атомов. Активно изучается взаимодействие атомов, особенно в твердых телах. Строению атомного ядра посвящена статья.
Вихман Э. Квантовая физика. М., 1977
Джеммер М. Эволюция понятий квантовой механики. М., 1985
Ельяшевич М.А. Атом; Атомная физика; Атомные спектры. Физическая энциклопедия, т. 1. М., 1988
Ответь на вопросы викторины «Неизвестные подробности»