ПАРАДОКСЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

ПАРАДОКСЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. Под словом «парадоксы» в данном случае понимают те выводы из СТО, которые, хотя и являются совершенно правильными по существу и подтверждаются экспериментами, тем не менее противоречат интуитивным, основанным на классической физике представлениям.

Два вывода из постулатов СТО (кстати, экспериментально подтвержденные) всегда вызывали особый интерес, хотя на практике с ними почти не приходится сталкиваться явно (неявно эти эффекты содержатся в любой релятивистской формуле).

Все дело в том, что эти выводы, на первый взгляд, совершенно не могут соответствовать реальности.

1. Самый известный – парадокс близнецов обычно формулируется так. Пусть брат-близнец А отправляется в космический полет на звезду Х, находящуюся от нас на расстоянии, скажем, 20 световых лет. Скорость звездолета близка к скорости света: v = 0,9с. Долетев до звезды примерно за 22,3 года (по своим часам), корабль разворачивается и летит обратно. Таким образом, по часам брата А, совершившего этот полет, прошло примерно T = 44,6 года. Второй брат-близнец Б дожидался возвращения брата А на Земле. У трапа звездолета брата А встретил дряхлый старец, которому пришлось ждать встречи более 100 лет.

Собственно, здесь еще нет парадокса. Действительно, при движении со скоростью v = 0,9c лоренц-фактор равен g » 2,3 и вследствие эффекта замедления времени по часам земного наблюдателя прошло время, равное gT » 103 года.

Парадокс возникает при попытке обратить рассуждение. Ведь с точки зрения брата А (неподвижный наблюдатель) движется брат Б, и по его часам проходит больше времени. Но с точки зрения брата Б движется брат А, и по его часам должно пройти больше времени. Таким образом, брат А должен вернуться постаревшим. Казалось бы, формулы СТО симметричны относительно замены v на –v. В чем же дело?

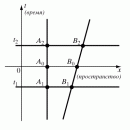
Этот парадокс разрешается следующим образом. Дело в том, что мировые линии братьев А и Б различны. Один из них (Б) находится в покое, другой (А) совершает движение с постоянной скоростью, которая в определенный момент изменяется на обратную, что возможно только при торможении и последующем ускорении космического корабля (что соответствует движению в неинерциальной системе отсчета). Таким образом, брат А движется от Земли и к Земле, находясь в покое сначала относительно одной инерциальной системы, а затем — относительно другой, и по дороге переходит на короткое время в неинерциальную систему. В то же время брат Б покоится относительно одной и той же инерциальной системы. Видно, что А и Б находятся в разных физических условиях, и это разрешает парадокс. Точный расчет показывает, что с точки зрения любого из братьев постареет больше тот, который неподвижен относительно Земли.

В ускорителях коротко живущие частицы, движущиеся со скоростями, близкими к скорости света, «живут» много дольше, чем «покоящиеся» частицы

2. Другой эффект – лоренцевское сокращение длины и связанные с ним парадоксы.

Пусть есть две инерциальные системы отсчета – S' и S. В системе S' жесткий стержень длиной Dx' покоится вдоль оси x и нужно определить его длину в системе S, относительно которой стержень движется со скоростью v. Чтобы измерить длину стержня в любой инерциальной системе, относительно которой стержень движется вдоль продольной оси, нужно одновременно наблюдать его концы. Это – ключевое положение, непонимание которого и приводит иногда к парадоксам.

В СТО нужно отличать то, что видит наблюдатель, от того, что он знает как бы пост-фактум. То, что наблюдатель видит или фотографирует в любой фиксированный момент времени, называется картиной мира в этот момент. Это понятие практически не очень важно, а теоретически очень сложно, т.к. то, что наблюдатель видит в данный момент, – это смесь событий, происходивших все дальше в прошлом и все дальше в пространстве.Если смотреть на ночное небо, полное звезд, то расстояния до этих звезд составляют от нескольких до сотен тысяч св. лет, следовательно, наблюдающий видит свет от этих звезд, испущенный в разное время и одновременно дошедший до его глаза, т.е он. видит разновременные события.

Полезнее понятие карты мира. Ее можно представлять как карту событий в сечении 4-мерного пространства Минковского плоскостью постоянного времени t = t0. Карта мира – это как бы трехмерный мгновенный фотоснимок в натуральную величину, сделанный одновременно везде, застывшее мгновение в пространственной системе отсчета наблюдателя. Реализовать такую карту мира могут совместные снимки, сделанные вспомогательными наблюдателями, размещенными в узлах пространственной решетки в данной инерциальной системе, причем каждый фотографирует свою окрестность в заранее обусловленный момент времени t = t0, а потом снимки склеиваются.

Когда говорят, что длина тела в системе S равна такой-то величине, речь идет о карте мира, т.е. об одновременной фиксации положений концов стержня в заданный момент времени. То, что на самом деле видит глаз, наблюдая движущееся тело, совершенно другой и не очень существенный вопрос.

Для вывода формулы сокращения длины преобразования Лоренца от системы S к системе S' записываются для приращений координат:

Dxў0 = g(Dx0 – vDx1), Dxў1 = g(Dx1 – vDx0).

Во второй формуле нужно положить Dx0 = 0 (одновременная фиксация концов стержня в системе S!). Тогда Dxў1 = gDx1. Если обозначить Dxў1 = L0, а Dx1 = L, то

L = L0/g ,

(g – лоренц-фактор).

Все парадоксы сокращения длины связаны, конечно, с симметрией эффекта: если наблюдатель в S видит сокращение длины, то и наблюдатель в S' должен видеть то же самое. Из «парадоксов» СТО можно сделать важный вывод: какой бы результат ни получился путем корректных рассуждений в некоторой инерциальной системе отсчета, он является верным в любой другой инерциальной системе отсчета.

При правильном использовании, СТО не допускает никаких «парадоксов».

Некоторые кажущиеся очевидными вещи оказываются совсем не такими очевидными в рамках СТО. Например, казалось бы, если вдоль оси x летит куб заданного размера, то, в силу лоренцовского сокращения, он должен в лабораторной системе выглядеть сплющенным в направлении движения, превратившимся в параллелепипед. Подробный расчет показывает, однако, что это не так: видимый куб не меняет своих размеров и только поворачивается на некоторый угол относительно оси x. Этот результат («невидимость лоренцова сокращения») был получен только через пятьдесят лет после создания СТО.

Александр Берков