НЕБЕСНАЯ МЕХАНИКА
НЕБЕСНАЯ МЕХАНИКА, раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается предвычислением положения Луны и планет, предсказанием места и времени затмений, в общем, определением реального движения космических тел.
Естественно, что небесная механика в первую очередь изучает поведение тел Солнечной системы – обращение планет вокруг Солнца, спутников вокруг планет, движение комет и других малых набесных тел. Тогда как перемещение далеких звезд удается заметить, в лучшем случае, за десятилетия и века, движение членов Солнечной системы происходит буквально на глазах – за дни, часы и даже минуты. Поэтому его изучение стало началом современной небесной механики, рожденной трудами И.Кеплера (1571–1630) и И.Ньютона (1643–1727). Кеплер впервые установил законы планетного движения, а Ньютон вывел из законов Кеплера закон всемирного тяготения и использовал законы движения и тяготения для решения небесно-механических проблем, не охваченных законами Кеплера. После Ньютона прогресс в небесной механике в основном заключался в развитии математической техники для решения уравнений, выражающих законы Ньютона. Таким образом, принципы небесной механики – это «классика» в том смысле, что и сегодня они такие же, как во времена Ньютона.
Законы движения Ньютона.
Чтобы лучше понять методы и результаты небесной механики, познакомимся с законами Ньютона и проиллюстрируем их простыми примерами.
Закон инерции.
Согласно этому закону, в системе отсчета, движущейся без ускорения, каждое тело сохраняет состояние покоя или прямолинейного и равномерного движения, если на него не действует внешняя сила. Это противоречит положению аристотелевой физики, утверждающему, что для поддержания движения тела требуется сила. Закон Ньютона говорит, что внешняя сила необходима только для приведения тела в движение, для его остановки или для изменения направления и величины его скорости. Темп изменения скорости тела по величине или направлению называется «ускорением» и свидетельствует о том, что на тело действует сила. Для небесных тел обнаруженное из наблюдений ускорение служит единственным указателем действующей на них внешней силы. Понятие о силе и ускорении позволяет с единой позиции объяснить движение всех тел в природе: от теннисного мяча до планет и галактик.
Поскольку объект, движущийся по искривленной траектории, испытывает ускорение, было заключено, что Земля на ее орбите вокруг Солнца постоянно подвергается влиянию силы, которую назвали «гравитацией». Задача небесной механики состоит в том, чтобы определить действующую на небесное тело силу гравитации и выяснить, как она влияет на его движение.
Закон силы.
Если к телу приложена сила, то оно движется ускоренно, причем чем больше сила, тем больше ускорение. Однако одна и та же сила вызывает различное ускорение у разных тел. Характеристикой инертности тела (т.е. сопротивления ускорению) служит его «масса», которую в первом приближении можно определить как «количество вещества»: чем больше масса тела, тем меньше его ускорение под действием заданной силы. Таким образом, второй закон Ньютона утверждает, что ускорение тела пропорционально приложенной к нему силе и обратно пропорционально его массе. Если из наблюдений известны ускорение тела и его масса, то, используя этот закон, можно вычислить действующую на тело силу.
Закон противодействия.
Этот закон утверждает, что взаимодействующие тела прилагают друг к другу равные по величине, но противоположно направленные силы. Поэтому в системе из двух тел, влияющих друг на друга одинаковой по величине силой, каждое испытывает ускорение, обратно пропорциональное его массе. Значит, лежащая на прямой между ними точка, удаленная от каждого обратно пропорционально его массе, будет двигаться без ускорения, несмотря на то, что каждое из тел движется ускоренно. Эту точку называют «центром масс»; вокруг нее обращаются звезды в двойной системе. Если одна из звезд вдвое массивнее другой, то она движется вдвое ближе к центру масс, чем ее соседка.
Законы Кеплера.
Чтобы изучать движение небесных тел, познакомимся с силой гравитации. Лучше всего это сделать на примере взаимного движения двух тел: компонентов двойной звезды или Земли вокруг Солнца (для простоты предполагая, что другие планеты отсутствуют). К таким системам применимы законы Кеплера. В основе их лежит тот факт, что оба взаимодействующих тела движутся в одной плоскости. Это означает, что и сила гравитации всегда лежит в той же плоскости.
Закон эллипсов.
Первый закон Кеплера утверждает, что планеты Солнечной системы движутся по эллипсам, в одном из фокусов которого находится Солнце. Фактически этот закон справедлив только для системы из двух тел, например для двойной звезды. Но и в Солнечной системе он выполняется довольно точно, поскольку на движение каждой планеты в основном влияет массивное Солнце, а все остальные тела влияют несравненно слабее.
Закон площадей.
Если отмечать не только положение планеты, но и время, то можно узнать не только форму орбиты, но и характер движения планеты по ней. Оно подчиняется второму закону Кеплера, утверждающему, что линия, соединяющая Солнце и планету (или компоненты двойной звезды), за равные интервалы времени «заметает» равные площади. Например, эта линия между Солнцем и Землей каждые сутки заметает 2ґ1014 квадратных километров. Из закона площадей следует, что Солнце притягивает планету строго по прямой, соединяющей их центры. Верно и обратное: для любой центральной силы справедлив второй закон Кеплера.
Рассмотрим планету (рис. 1), перемещающуюся из точки A в B за единицу времени. Если бы притяжение к точке O, где расположено Солнце, отсутствовало, то за следующую единицу времени планета переместилась бы в точку Y, такую, что AB = BY. С другой стороны, при наличии притяжения покоящееся в точке B тело переместилось бы за это время на расстояние x. Чтобы найти точку C, в которую действительно переместится планета, проведем прямую CY длиной x параллельно OB. Перпендикуляры, опущенные из точек Y и C на отрезок OB, очевидно, равны между собой. Если отрезок YD есть перпендикуляр из точки Y, а отрезок AE – перпендикуляр из точки A, то и они равны между собой из равенства треугольников YDB и AEB. Следовательно, высоты треугольников OBC и OBA равны, а значит, равны и площади этих треугольников, поскольку OB – их общее основание. Тем самым мы доказали, что за равные времена прямая, соединяющая планету с Солнцем (ее называют «радиусом-вектором» планеты), заметает равные площади. Если бы сила притяжения не была направлена точно к Солнцу, то отрезок CY не был бы параллелен прямой OB, и наше доказательство не было бы справедливым.
Разумеется, приведенное выше доказательство справедливо лишь для бесконечно малых значений углов BOC и BOA. Однако любой отрезок орбиты можно представить как последовательность большого числа таких фигур, поэтому и для него доказательство останется справедливым.
Гармонический закон.
Еще больше можно узнать о силе гравитации из третьего закона Кеплера, связывающего размер планетной орбиты с периодом обращения по ней. Его называют гармоническим законом, поскольку склонный к мистике Кеплер считал эту связь проявлением «небесной гармонии». Закон гласит, что если а – большая полуось эллиптической орбиты планеты, а P – период обращения по ней, то отношение a3/P2 одинаково для всех планет.
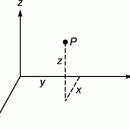
Рассмотрим некоторую планету, обращающуюся вокруг Солнца по круговой орбите радиуса a. Солнце притягивает ее с постоянной по величине силой, сообщая ускорение, необходимое для равномерного изменения направления движения. Найдем это ускорение, вычислив изменение скорости планеты V за единицу времени (рис. 2). За период оборота планеты по орбите, равный 2pa/V, вектор скорости совершает полный поворот. Поэтому изменение скорости за это время равно длине окружности радиуса V. Изменение скорости за единицу времени, т.е. ускорение, составляет
Обозначив орбитальный период через P, мы можем записать скорость как V = 2pa/Р. Тогда из выражения для ускорения получим, что оно пропорционально (a/P)2/a, или a/P2. Домножив числитель и знаменатель на a2, запишем это выражение так: (a3/P2)Ч(1/a2). Но, согласно гармоническому закону Кеплера, первый сомножитель постоянен – его значение одинаково для всех тел Солнечной системы. Значит, центростремительное ускорение и вызывающая его сила гравитации пропорциональны второму сомножителю, т.е. изменяются обратно пропорционально квадрату расстояния от Солнца. (Хотя мы доказали это только для круговой орбиты, более изощренные математические методы позволяют доказать это и для эллиптических орбит.)
Гармонический закон утверждает, что период обращения планеты зависит только от ее расстояния от Солнца и не зависит от ее массы. Значит, все тела, движущиеся по одной орбите, должны иметь одинаковую скорость.
Закон всемирного тяготения Ньютона.
Анализируя законы Кеплера и наблюдательные данные о движении Луны, Ньютон сформулировал новый закон: каждая частица вещества притягивается к любой другой частице вдоль соединяющей их прямой с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Это всеобщий закон; он не ограничен влиянием Солнца на планеты. Он описывает также взаимодействие двух звезд, планеты и ее спутника, Земли и метеорита, Солнца и кометы. Все вещество во Вселенной подчиняется этому закону, поэтому его называют законом всемирного тяготения. Всеобщность этого закона дополняется его уникальностью: как доказали математики, планетные орбиты имеют вид эллипсов, в фокусе которых находится Солнце, только в том случае, если притяжение меняется обратно пропорционально квадрату расстояния.
Казалось бы, попытка на основе ньютоновых законов движения и гравитации исследовать относительное движение взаимно притягивающихся тел должна привести к выводу знакомых нам законов Кеплера. Но это решительно не так, ибо законы Кеплера справедливы только в том случае, если: 1) взаимодействуют не более двух тел; 2) тела движутся по замкнутым орбитам; 3) масса одного из тел пренебрежимо мала по сравнению с массой другого. Эти условия делают анализ предельно простым, но они совершенно не обязательны для применения законов движения и гравитации. Используя эти общие законы, мы можем пренебречь указанными ограничениями. Сделаем это, отказываясь каждый раз лишь от одного из них.
Во-первых, можно показать, что орбита может быть не только эллипсом (частный случай которого – окружность), но также параболой или гиперболой. Все эти кривые называют «коническими сечениями», поскольку они получаются при пересечении прямого кругового конуса плоскостью. Круг и эллипс – замкнутые кривые; парабола и гипербола – незамкнутые. Спутник, движущийся по замкнутой орбите, совершает одинаковые обороты снова и снова, а спутник, движущийся по незамкнутой кривой, приближается к главному телу с бесконечно далекого расстояния и, пролетев поблизости от него, вновь удаляется на бесконечность.
Во-вторых, можно показать, что «постоянная» величина a3/P2 в гармоническом законе численно равна сумме масс двух взаимодействующих тел, если a выражено в расстояниях Земли от Солнца (в астрономических единицах), P – в периодах обращения Земли (в годах), а масса – в сумме масс Земли и Солнца. Поскольку в Солнечной системе масса любой планеты не превосходит тысячной доли массы Солнца, величины a3/P2 для всех планет различаются не более чем на 0,1%. Будь планеты массивнее, Кеплер не смог бы сформулировать свой гармонический закон. В общем виде этот закон выглядит так:
где M и m – массы компонентов системы, например Земли и Луны или звезд в двойной системе, причем значения масс могут быть любыми. (Все значения величин в этой формуле должны быть выражены в единой системе, например: астрономическая единица, год, масса Солнца.) Этот закон астрономы используют для определения масс различных космических объектов.
Можно также исследовать поведение трех или более взаимно притягивающихся тел. Закон тяготения позволяет вычислить силу, действующую на каждое из тел со стороны остальных, а законы движения – определить, как изменяется от этого его скорость. В случае двух тел их траектории движения могут быть представлены простыми уравнениями Кеплера. Но если тел больше, то это невозможно сделать с помощью конечного числа уравнений.
Этот последний случай наиболее часто встречается в небесной механике Солнечной системы. Важную проблему трех тел представляет система Земля – Луна – Солнце, но и здесь для точного вычисления орбиты Луны приходится учитывать возмущения со стороны других планет (особенно Юпитера и Сатурна), влияние экваториального вздутия Земли и даже влияние приливов, которые Луна вызывает в океанах Земли.
Интерес к классической небесной механике значительно возрос в последние десятилетия в связи с необходимостью расчета орбит искусственных спутников и межпланетных аппаратов. Мощные компьютеры сделали возможным быстрое решение любой небесно-механической задачи с высокой точностью. Впервые для таких расчетов был использован компьютер SSEC фирмы IBM размером с комнату. Для вычисления положений Юпитера, Сатурна, Урана, Нептуна и Плутона с интервалом в 40 сут с 1653 по 2060 ему понадобилось 140 ч; сегодня рядовой компьютер делает это менее чем за 2 с. Теперь с помощью мощнейших компьютеров стало возможным решать такие задачи, которые были совершенно не доступны классической небесной механике: можно проследить на протяжении миллиардов лет эволюцию скопления, состоящего из сотен тысяч звезд; можно детально рассчитать, как исказится форма двух сталкивающихся галактик. Компьютер вдохнул новую жизнь в небесную механику.
Ответь на вопросы викторины «Астрономия»