УГЛЫ НА ПЛОСКОСТИ И ИХ ИЗМЕРЕНИЕ

УГЛЫ НА ПЛОСКОСТИ И ИХ ИЗМЕРЕНИЕ. Фигура на плоскости, образованная двумя лучами, исходящими из одной точки O, называется углом. Лучи OA и OB называются сторонами угла, а точка O вершиной. Угол со сторонами OA и OB обозначается РAOB.

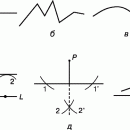
Углы сравнивают, складывают, измеряют. Они равны, если их можно совместить перемещением. Два угла называются смежными (рис. 1), если у них общие вершина и одна сторона, а две другие образуют прямую. Вообще, углы, имеющие общую вершину и одну общую сторону, называются прилежащими (рис. 2). Углы называются вертикальными (рис. 3), если стороны одного являются продолжениями за вершину сторон другого. Вертикальные углы равны между собой. Угол, у которого стороны образуют прямую, называется развернутым (рис. 4). Угол, равный своему смежному, называется прямым. Угол меньший прямого – острый, больший прямого, но меньший развернутого – тупой.

При пересечении двух прямых, лежащих в одной плоскости, третьей прямой образуются углы (рис. 5). 1 и 5, 2 и 6, 4 и 8, 3 и 7 называются соответственными; 2 и 5, 3 и 8 – внутренними односторонними; 1 и 6, 4 и 7 – внешними односторонними; 3 и 5, 2 и 8 – внутренними накрест лежащими; 1 и 7, 4 и 6 – внешними накрест лежащими.

Если луч OC проходит внутри угла AOB (рис. 6), то, по определению, считают, что угол AOC, как и угол COB, меньше угла AOB и что угол AOB равен сумме углов AOC и COB. Взяв за единицу измерения какой-либо конкретный угол, определяют величину любого угла, т.е. находят, сколько раз укладывается в нем данный единичный угол. При измерении угла исходят из двух его свойств, аналогичных свойствам длины отрезка: 1) величины равных углов равны, 2) величина суммы двух углов равна сумме их величин.

Если рассмотреть углы, вершиной которых является центр окружности, а сторонами – радиусы, то можно отметить, что равные углы высекают на окружности равные дуги, и сумме углов будет соответствовать сумма стягиваемых ими дуг. Поэтому величина угла пропорциональна длине высекаемой им дуги, и единицы измерения можно задавать, указывая, какую часть окружности составляет соответствующая дуга.

Обычно пользуются двумя системами измерения углов: градусной и радианной.

В градусной системе за единицу измерения принимают дугу размером в 1/360 окружности (обозначают °). Градус делится на 60 минут (обозначают '), минута на 60 секунд (обозначают ''). Шестидесятиричность измерений напоминает о Вавилоне, но был в истории еще один градус. Во времена Великой французской революции (1793) во Франции вместе с десятичной (метрической) системой мер была введена сотенная (центезимальная) система измерения углов. В ней прямой угол делится на 100 градусов («градов»), градус на 100 минут, минута на 100 секунд. Эта система наиболее часто применяется в геодезических измерениях.

Математики предпочитают пользоваться радианной мерой – за единицу измерения принимается угол, под которым видна из центра окружности ее дуга, равная радиусу. Величина такого угла и есть радиан. Она не зависит от радиуса окружности и от положения дуги на окружности. Т.к. полуокружность видна из центра под углом 180°, а ее длина равна 241 радиусам, то радиан в 241 раз меньше, чем угол 180°, т.е. один радиан равен 180°/241:

1 радиан » 57,2958° » 57°17'45''

И в радианной и в градусной системе угол измеряется единицей угла. То, что наименование в одном случае (для градуса) проставляется, а в другом (для радиана) подразумевается, не играет никакой роли.

Радианная мера, выражающаяся отношением длины дуги, описанной произвольным радиусом из центра и заключенной между сторонами угла, к радиусу этой дуги, не зависит от выбора единицы длины. Так же не зависит и градусная мера, т.к. она тоже является отношением двух длин, а именно длины дуги, описанной из вершины угла и заключенной между ее сторонами, к длине дуги равной 1/360 части окружности того же радиуса.

Таким образом, никакой принципиальной разницы между градусной и радианной мерой угла нет, однако введение радианной меры позволяет придать многим формулам более простой вид.

Соотношение градусной и радианной мер наиболее часто встречающихся углов приведено в следующей таблице

Соотношение градусной и радианной мер углов

Углы в градусах	360°	180°	90°	60°	45°	30°
Углы в радианах	2π	π	π/2	π/3	π/4	π/6

Прямой угол содержит в себе 90° или 241/2 радиан. Острый лежит в пределах от 0 до 90° или от 0 до 241/2 радиан, тупой – от 90 до 180° или от 241/2 до 241. Прямые линии, образующие прямой угол, называются перпендикулярными одна другой.

Часто важно указать, в каком направлении измеряется угол. Если рассматривать в качестве меры угла поворот вокруг вершины О, переводящий луч OA в положение OB, то положительной мера угла считается, если поворот происходит против часовой стрелки, в противном случае угол считается отрицательным. Таким образом, угол может иметь своей величиной любое действительное число. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.

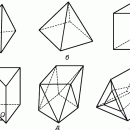
Под углом между двумя кривыми, выходящими из общей точки, в которой каждая из кривых имеет определенную касательную, понимают угол, образованный этими касательными. Понятие угла обобщается и на различные объекты в пространстве (двугранные, телесные и многогранные углы.