ВАН-ДЕР-ВААЛЬСА УРАВНЕНИЕ

ВАН-ДЕР-ВААЛЬСА УРАВНЕНИЕ – модельное уравнение состояния реального газа, учитывающее, в отличие от уравнения состояния идеального газа, взаимодействие молекул между собой, а именно: мощное отталкивание на малых расстояниях R между центрами масс молекул

() и их притяжение на больших

(R > R₁₂) расстояниях. Здесь R₁ и R₂ – газокинетические радиусы молекул. В ряде случаев, для простоты, используется средний газокинетический диаметр взаимодействующих молекул , очевидно для одинаковых молекул .

Уравнение состояния является функциональной связью между четырьмя термодинамическими параметрами состояния физической системы. Для описания однокомпонентных (состоящих из частиц одного сорта) физических систем достаточно четырех параметров. Для систем, состоящих из различных частиц (например, воздух – смесь азота, кислорода, аргона, углекислого газа и др.), полный перечень необходимых параметров включает относительные концентрации компонент смеси. Для простоты, будут рассмотрены только однокомпонентные системы. Традиционный и наиболее употребительный набор параметров состояния состоит из массы системы m, давления p, объема V и температуры T. Использование массы системы в качестве одного из ее параметров предполагает, что известна молярная масса вещества , из которого она состоит. Набор параметров состояния «продиктован» экспериментом, так как все входящие в него величины достаточно просто и непосредственно измеряются. Здесь число молей. Разумеется, возможны и другие наборы параметров состояния: число частиц в системе , объем, энтропия и внутренняя энергия (N_A – число Авогадро).

Уравнение состояния идеального газа (газа невзаимодействующих материальных точек) было получено Э.Клапейроном (1834) в результате объединения трех экспериментально установленных газовых законов: 1) Р.Бойля (1662) и Э.Мариотта (1676); 2) Шарля (1785); 3) Гей-Люссака (1802). Сейчас это уравнение (здесь R – универсальная газовая постоянная)

называют уравнением Клапейрона – Менделеева. 

В данном частном случае заслуга Д.И.Менделеева в том, что он вывел написанное выше универсальное уравнение состояния идеальных газов. В частности, при исследовании явлений, не укладывающихся в модель идеального газа и обусловленных взаимодействием молекул между собой (поверхностное натяжение жидкостей и сопутствующие капиллярные явления, непрерывные и скачкообразные фазовые переходы жидкость – газ), Менделеев ввел понятие температуры «абсолютного» кипения, которая впоследствии была названа Эндрюсом критической температурой – температурой критического состояния вещества, это уже сфера непосредственных применений уравнения Ван-дер-Ваальса.

Учет взаимодействия между молекулами газа при расчете его термодинамических характеристик впервые был выполнен в 1873 голландским физиком Я.Д.Ван-дер-Ваальсом, именем которого названо полученное им уравнение состояния такого газа. Строго говоря, ван-дер-ваальсовским можно называть газ, потенциальная энергия притяжения молекул которого на больших расстояниях убывает с ростом R по закону

(1) ,

его, например, нет места в плазме состоящей из заряженных частиц, потенциальная энергия взаимодействия которых на больших расстояниях убывает в соответствии с законом Кулона

(2) ,

т.е существенно медленнее.

Силы Ван-дер-Ваальса (R > d0)

(3)

для молекулярных и атомарных газов носят достаточно универсальный характер. Квантовомеханическое усреднение потенциальной энергии по взаимным ориентациям взаимодействующих объектов практически во всех случаях приводит к асимптотическому закону (1), (3).

Во-первых, это взаимодействие полярных молекул, т.е. молекул с собственным электрическим дипольным моментом (молекулы типа HCl, H₂O и т.п.). Соответствующие силы называют ориентационными.

Во-вторых, взаимодействие полярной и неполярной молекулы (не имеющей собственного электрического дипольного момента): He, Ar, … N₂, O₂ … . Такое взаимодействие принято называть индукционным.

Наконец, взаимодействие неполярных атомов и молекул – дисперсионное взаимодействие. Происхождение дисперсионных сил строго объясняется только в рамках квантовой механики. Качественно возникновение этих сил можно объяснить – в результате квантовомеханических флуктуаций у неполярной молекулы возникает мгновенный дипольный момент, его электрическое поле поляризует другую неполярную молекулу и у неё появляется наведенный мгновенный дипольный момент. Энергия взаимодействия неполярных молекул – это квантовомеханическое среднее энергии взаимодействия таких мгновенных диполей. Дисперсионные силы не зависят от наличия или отсутствия собственных дипольных моментов у атомов и молекул и потому всегда имеют место. В случае неполярных атомов и молекул дисперсионные силы в десятки и даже сотни раз больше сил ориентационных и индукционных. В случае молекул с большим собственным дипольным моментом, например, молекул воды H₂O, дисперсионная сила в три раза меньше ориентационной. Все эти силы имеют асимптотику (3), таким образом, в общем случае усредненная потенциальная энергия

(4)   при   .

Мощное отталкивание молекул на малых расстояниях возникает при перекрытии внешних заполненных электронных оболочек и обусловлено принципом запрета Паули. Зависимость этих сил от R нельзя объяснить в рамках чисто классической электродинамики. Силы отталкивания в большей мере, чем силы притяжения, зависят от конкретных особенностей строения электронных оболочек взаимодействующих молекул и требуют для своего определения громоздких квантовомеханических расчетов. Хорошее согласие с экспериментом дает следующая модель

(5) .

Из (5) видно, что уменьшение расстояния в два раза приводит к увеличению силы отталкивания 15 более чем в 8 тысяч раз, что и позволяет говорить о «мощных» силах отталкивания.

При практических расчетах широко используется модельный потенциал Ленард – Джонса, (с учетом (1) и (5))

(6) ,

показанный на рис. 1. Видно, что параметр D имеет смысл глубины потенциальной ямы, а параметр
определяет ее размер: абсцисса минимума .

Уравнение состояния ван-дер-ваальсовского газа, само по себе приближенное, может быть, тем не менее, точно получено в рамках модели притягивающихся твердых шаров. В этой модели весьма большие, но конечные силы отталкивания на малых расстояниях заменяются бесконечно большими силами, что означает замену близкого к вертикали криволинейного потенциального ба­­рь­ера левее точки минимума (рис. 1) вертикальной потенциальной стенкой в соответствующей точке: R = d₀, что показано на рис. 2. При расстояниях сохраняется зависимость от R по формуле (6).

Вертикальная потенциальная стенка ставится именно в точке R = d₀ = 2R₀, т.к. минимальное расстояние между центрами двух твердых шаров равно их диаметру.

Притяжение молекул на расстояниях дает поправку к внутренней энергии газа, равную энергии их взаимодействия: U_вз. При достаточной разреженности газа с хорошей точностью справедливо предположение о попарном взаимодействии молекул, что приводит к выражению для Uвз:

(7) , 24

Где одна из двух постоянных Ван-дер-Ваальса, учитывающая притяжение между молекулами, N – число молекул в газе, V – объем газа. Можно просто объяснить аналитическую структуру выражения (7). Число молекул в единице объема , взаимодействуют они попарно, число пар молекул в единице объема , что, учитывая макроскопичность n, можно считать точно равным . Средняя энергия взаимодействия одной пары молекул, как видно из структуры интеграла в (7), равна , откуда для объема V, в силу аддитивности энергии, получается   , т.е. формула (7).

Внутренняя энергия реального газа складывается из суммарной кинетической энергии его молекул (той же, что и в идеальном газе при тех же параметрах состояния) и потенциальной энергии их взаимодействия. Отсюда, например, для одноатомного газа с температурой T можно записать:

(8) .

Конечность объема молекул приводит к тому, что не весь объем сосуда V доступен для их движения – уменьшается «свобода» размещения молекул газа в его фазовом пространстве, что, в свою очередь, уменьшает статистический вес макросостояния и энтропию газа. Энтропия идеального (молекулы – материальные точки) одноатомного газа с температурой , занимающего сосуд объемом V, имеет вид

(9)    

Если объем недоступный для движения молекул – шариков реального газа, равен V₀, то его энтропия

(10)  

Для двух молекул радиуса R₀ с минимальным расстоянием между центрами 2R₀, объем, недоступный для движения, – это объем сферы, равный

, где – учетверенный объем одной молекулы, это вторая константа Ван-дер-Ваальса.

Недоступный для движения объем в расчете на одну молекулу равен , а для N молекул –

, откуда окончательное выражение для энтропии одноатомного ван-дер-ваальсовского газа имеет вид

,  

В рамках рассматриваемой модели параметры а и b (вторые формулы в (8) и (12)) являются атомными константами (диаметр молекулы d₀ считается фиксированной величиной, не зависящей от температуры, хотя, строго говоря, это не так), не зависящими параметров термодинамического состояния вещества.

Основное термодинамическое тождество имеет вид

(12) dU = TdS – pdV,

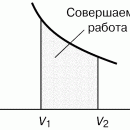
это первое начало термодинамики, в которое для квазистатических процессов подставлены выражения для получаемой системой теплоты и (–pdV) для совершаемой над системой работы, оно позволяет получить уравнение состояния Ван-дер-ваальсовского газа с выражения для давления, следующего из (12)

(13).  

В (13) индекс S указывает на то, что дифференцировать нужно при постоянной энтропии. Подстановка (8) и (11) в (13) приводит к уравнению состояния реального газа Ван-дер-Ваальса

(14) . 

Переход от числа молекул в газе N к числу молей осуществляется с помощью замены , где N_A – число Авогадро и соответствующего этой замене переопределения постоянных Ван-дер-Ваальса

(15). 

В этих переменных уравнение Ван-дер-Ваальса имеет вид ( универсальная газовая постоянная):

(16).

Главное значение уравнения Ван-дер-Ваальса состоит, во-первых, в простоте и физической понятности его аналитической структуры: поправка a учитывает притяжение молекул на больших расстояниях, поправка b – их отталкивание на малых расстояниях. Уравнение состояния идеального газа получается из (16) путем предельного перехода a → 0, b → 0. стрелки

Во-вторых, уравнение Ван-дер-Ваальса обладает (несмотря на приближенность модели) широким спектром качественных, а в ряде случаев и полуколичественных предсказаний о поведении реального вещества, которые следуют из анализа уравнения (16) и вида соответствующих ему изотерм и касаются поведения вещества не только в достаточно разреженном газообразном состоянии, но и в жидком и двухфазном состояниях, т.е. в состояниях, далеких от априорной области применимости модели Ван-дер-Ваальса.

Рис. 3. Изотермы Ван-­дер-Ваальса. Цифры, указывают отношение температуры, соответствующей данной изотерме, к критической тем­пературе вещества. Единица соответствует критической изотерме T = T_кр.

Уравнение (16) имеет особую точку – точку перегиба, в которой

(17). ,

это соответствует реальной физической особенности – критическому состоянию вещества, в котором исчезает различие между жидкостью и ее паром (жидкой и газовой фазами), находящимися в состоянии термодинамического равновесия. Критическая точка является одним из концов кривой равновесия жидкость – пар на диаграмме (p, T), другим концом этой кривой является тройная точка, в которой в термодинамическом равновесии находятся все три фазы: газовая, жидкая и кристаллическая. Критической точке соответствуют критическая температура T_кр., критическое давление pкр. и критический объем V_кр. При температурах выше критической переход «жидкость – пар» происходит без скачка плотности, в критической точке исчезает мениск в капилляре, обращается в нуль теплота испарения и в бесконечность изотермическая сжимаемость (пропорциональная производной ).

Решение уравнений (17) дает связь критических параметров с постоянными Ван-дер-Ваальса a и b:

(18). .

Формулы (18) позволяют найти константы а и b по экспериментально определенным параметрам критического состояния. Одним из показателей количественной точности уравнения Ван-дер-Ваальса является результат критического коэффициента , следующего из (18) c его экспериментальным значением

Вещество	Kкр, эксперимент	Вещество	Kкр, эксперимент
H2	3,03	SO2	3,60
He	3,13	C6H6	3,76
N2	3,42	H2O	4,46
O2	3,42	CO2	4,49

Если для водорода , то для углекислого газа это отношение уже составляет .

Критическое давление и критическая температура, например, воды равны соответственно: ,   .

На рис. 4 дано несколько утрированное (по сравнению с рис. 3) качественное изображение изотермы Ван-дер-Ваальса с температурой ниже критической. На участке 3–4–5 производная , что нереализуемо. Вещество в таком состоянии существовать не может, так как оно термодинамически неустойчиво: увеличение объема при постоянной температуре приводит к увеличению давления. Невозможность существования вещества в таком состоянии вытекает и из второго начала термодинамики, из которого строго следует, что для любого вещества изотермическая производная может быть только меньше нуля, это плата за интерполя­ционный характер модели Ван-дер-Ваальса. Поправка к энергии рассчитана в предположении парности

взаимодействия молекул, что справедливо при малых плотностях (больших объемах) – это «хвост» 6–7 изотермы на рис. 4, где она асимптотически сближается с изотермой идеального газа. Поправка на конечность размера молекул сделана в предположении, что молекулы ведут себя как твердые шары, это приближенно имеет место в жидкости при объемах, близких к суммарному объему плотно упакованных молекул, чему соответствует участок 1–2 изотермы. Следовательно, только на «концах» 1–2 и 6–7 изотермы ван-дер-ваальсовский подход может претендовать на приближенное количественное и правильное качественное описание. В промежуточной области теоретических оснований для таких претензий нет и, как следствие, получается нефизический участок 3–4–5.

Таким образом, участок 1–2 может быть поставлен в соответствие жидкому состоянию вещества. Его вертикальность обусловлена тем, что при V стрелка vb знаменатель в первом слагаемом (16) обращается в нуль и кривая выходит на вертикальную асимптоту V = vb = V₀. В эксперименте этому соответствует ничтожно малая (по сравнению с газами) сжимаемость жидкостей. На участке 6–7 изотерма Ван-дер-Ваальса близка к изотерме идеального газа.

При температурах ниже критической, когда только и есть нефизический участок 3–4–5 (см. рис. 3), переход из жидкого состояния 1–2 в газовое состояние 6–7 происходит только через двухфазное состояние. Известно, что давление в двухфазной системе есть однозначная функция температуры, поэтому в переменных (p, V) соответствующий двухфазному состоянию На рис. 4 участок изотермы является отрезком горизонтальной прямой (участок 2–4–6 на рис. 4).

В уравнении Ван-дер-Ваальса нет горизонтального участка, однако наличие ван-дер-ваальсовского нефизического участка 3–4–5 позволяет теоретически определить «высоту» двухфазного участка 2–4–6, т.е. давление в двухфазной системе при данной температуре.

Если рассмотреть циклический процесс 2–3–4–5–6–4–2 (замкнутый контур ) и, учитывая, что во всех точках этого цикла температура постоянна, проинтегрировать основное термодинамическое тождество, то получим
(19) .

Равенство нулю интегралов в правой части (19) есть следствие замкнутости процесса и того, что энтропия S и внутренняя энергия U – функции состояния. Равенство нулю интеграла означает, что двухфазный участок следует расположить так, чтобы площади S₁ и S₂ (рис. 4) были равны (правило Максвелла).

Участки 2–3 и 5–6 соответствуют реальным метастабильным состояниям вещества, а именно: 2–3 – перегретая жидкость, 6–5 – переохлажденный (пересыщенный) пар. В этих состояниях жидкость или пар могут существовать в течение некоторого времени, если нет центров парообразования и конденсации. Появление в жидкости центров парообразования ведет к немедленному возникновению и росту на их месте пузырьков пара. Аналогично, появление центров конденсации в переохлажденном паре ведет к немедленному возникновению и росту на их месте капель жидкости. Оба явления используются для регистрации треков заряженных частиц: первое в пузырьковой камере, второе в камере Вильсона (туманной камере). Роль центров парообразования (конденсации) играют ионы, которые оставляет на своем пути заряженная частица в результате ионизации молекул жидкости (пара) при столкновениях с ними. Пузырьки (капли) существуют достаточное для их фотографирования время, что делает видимой траекторию, по которой двигалась заряженная частица. Исследование трека частицы позволяет определить ее энергию и импульс, соответственно, вычислить ее массу, что является одной из важнейших задач физики элементарных частиц.

При температуре , что для воды составляет 273° C, минимум ван-дер-ваальсовской изотермы достигает нуля давления. При более низких температурах (рис. 3, кривые 0,8 и 0,7) давление в окрестности минимума становится отрицательным, что означает, что жидкость из-за действия сил притяжения между ее молекулами может «сопротивляться растяжению» (подобно пружине). Растянутую жидкость (например, ртуть) можно получить экспериментально, беря запаянную с одного конца стеклянную трубку длиной около метра и погружая ее в горизонтальную кювету с ртутью. После заполнения трубки ртутью трубку медленно, без встряхиваний поднимают в вертикальное положение, при этом в трубке наблюдается столб ртути, длина которого заметно превышает длину, соответствующую внешнему давлению, например, 760 мм.

Валериан Гервидс