АРИФМЕТИКА

Содержание статьи

• Краткая история арифметики.
• Механизация арифметических вычислений.
• Целые положительные числа.
• Делители целых чисел.
• Положительные рациональные числа.
• Положительные действительные числа.
• Индо-арабская система счисления.
• Названия чисел.
• Сложение.
• Вычитание.
• Умножение.
• Деление.
• Дроби.
• Квадратный корень.
• Кубический корень.
• Алгоритм Евклида.
• Проверка.
• Проценты.
• Арифметика приближенных чисел.
• Логарифмы.

АРИФМЕТИКА, искусство вычислений, производимых с положительными действительными числами.

Краткая история арифметики.

С глубокой древности работа с числами подразделялась на две различные области: одна касалась непосредственно свойств чисел, другая была связана с техникой счета. Под «арифметикой» во многих странах обычно имеется ввиду именно эта последняя область, которая несомненно является старейшей отраслью математики.

По-видимому, наибольшую трудность у древних вычислителей вызывала работа с дробями. Об этом можно судить по папирусу Ахмеса (называемому также папирусом Ринда), древнеегипетскому сочинению по математике, датируемому примерно 1650 до н.э. Все дроби, упоминаемые в папирусе, за исключением 2/3, имеют числители, равные 1. Трудность обращения с дробями заметна и при изучении древневавилонских клинописных табличек. И древние египтяне, и вавилоняне, по-видимому, производили вычисления с помощью некоторой разновидности абака. Наука о числах получила у древних греков существенное развитие начиная с Пифагора, около 530 до н.э. Что же касается непосредственно техники вычисления, то в этой области греками было сделано гораздо меньше.

Жившие позднее римляне, напротив, практически не внесли никакого вклада в науку о числе, зато исходя из нужд быстро развивавшихся производства и торговли усовершенствовали абак как счетное устройство. О зарождении индийской арифметики известно очень мало. До нас дошли лишь некоторые более поздние работы о теории и практике операций с числами, написанные уже после того, как индийская позиционная система была усовершенствована посредством включения в нее нуля. Когда в точности это произошло, нам достоверно неизвестно, но именно тогда были заложены основы для наших наиболее распространенных арифметических алгоритмов (см. также ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ).

Индийская система счисления и первые арифметические алгоритмы были заимствованы арабами. Самый ранний из дошедших до нас арабских учебников арифметики был написан аль-Хорезми около 825. В нем широко используются и объясняются индийские цифры. Позднее этот учебник был переведен на латынь и оказал значительное влияние на Западную Европу. Искаженный вариант имени аль-Хорезми дошел до нас в слове «алгоризм», которое при дальнейшем смешении с греческим словом аритмос превратилось в термин «алгоритм».

Индо-арабская арифметика стала известна в Западной Европе в основном благодаря сочинению Л.Фибоначчи Книга абака (Liber abaci, 1202). Метод абацистов предлагал упрощения, подобные использованию нашей позиционной системы, во всяком случае для сложения и умножения. Абацистов сменили алгоритмики, которые использовали нуль и арабский метод деления и извлечения квадратного корня. Один из первых учебников арифметики, автор которого нам неизвестен, вышел в Тревизо (Италия) в 1478. В нем речь шла о расчетах при совершении торговых сделок. Этот учебник стал предшественником многих появившихся впоследствии учебников арифметики. До начала 17 в. в Европе было опубликовано более трехсот таких учебников. Арифметические алгоритмы за это время были существенно усовершенствованы. В 16–17 вв. появились символы арифметических операций, такие как =, +, -, ґ, ё и .

Принято считать, что десятичные дроби изобрел в 1585 С.Стевин, логарифмы – Дж.Непер в 1614, логарифмическую линейку – У.Оутред в 1622. Современные аналоговые и цифровые вычислительные устройства были изобретены в середине 20 в. См. также МАТЕМАТИКИ ИСТОРИЯ; ЧИСЕЛ ТЕОРИЯ; РЯДЫ.

Механизация арифметических вычислений.

С развитием общества росла и потребность в более быстрых и точных вычислениях. Эта потребность вызвала к жизни четыре замечательных изобретения: индо-арабские числовые обозначения, десятичные дроби, логарифмы и современные вычислительные машины.

На самом деле простейшие счетные устройства существовали до появления современной арифметики, ибо в древности элементарные арифметические операции производились на абаке (в России с этой целью использовались счеты). Простейшим современным вычислительным устройством можно считать логарифмическую линейку, представляющую собой две скользящие одна вдоль другой логарифмические шкалы, что позволяет производить умножение и деление, суммируя и вычитая отрезки шкал. Изобретателем первой механической суммирующей машины принято считать Б.Паскаля (1642). Позднее в том же столетии Г.Лейбниц (1671) в Германии и С.Морленд (1673) в Англии изобрели машины для выполнения умножения. Эти машины стали предшественницами настольных вычислительных устройств (арифмометров) 20 в., позволявших быстро и точно производить операции сложения, вычитания, умножения и деления.

В 1812 английский математик Ч.Бэббидж приступил к созданию проекта машины для вычисления математических таблиц. Хотя работа над проектом продолжалась долгие годы, она так и осталась незавершенной. Тем не менее проект Бэббиджа послужил стимулом к созданию современных электронных вычислительных машин, первые образцы которых появились около 1944. Быстродействие этих машин поражало воображение: с их помощью за минуты или часы удавалось решить задачи, ранее требовавшие многих лет непрерывных вычислений даже с применением арифмометров.

Суть дела можно пояснить на примере конкретной арифметической задачи, например, вычисления числа p (отношения длины окружности к ее диаметру). Первые систематические попытки вычисления p встречаются у Архимеда (ок. 240 до н.э.). Используя весьма несовершенную систему счисления, он после долгих трудов сумел вычислить p с точностью, эквивалентной в нашей современной системе счисления двум знакам после запятой. Используя метод Архимеда, Л.ван Цейлен (1540–1610), посвятив этому значительную часть жизни, сумел вычислить p с точностью 35 знаков после запятой. В 1873 после пятнадцати лет работы У.Шенкс получил значение p с 707 знаками, но позднее выяснилось, что начиная с 528-го знака в его вычисления вкрались ошибки. В 1958 компьютер фирмы ИБМ вычислил за 40 секунд 707 знаков числа p и, продолжая далее вычисления, получил за 100 минут 10000 знаков. См. также КОМПЬЮТЕР; ЧИСЛО p.

Целые положительные числа.

Основой наших представлений о числах являются интуитивные понятия множества, соответствия между множествами и бесконечной последовательности различимых знаков или звуков. Знакомая всем нам последовательность символов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ... есть не что иное, как бесконечная последовательность различимых знаков и бесконечная последовательность различимых звуков (или слов) «один», «два», «три», «четыре», «пять», «шесть», «семь», «восемь», «девять», «десять», «одиннадцать», «двенадцать», ..., соответствующих определенным символам. Любое множество, все элементы которого можно поставить во взаимно однозначное соответствие с элементами некоторого начального сегмента нашей бесконечной последовательности символов, называется конечным множеством. При этом на число элементов множества указывает последний символ сегмента. Например, множество предметов, которые можно поставить во взаимно однозначное соответствие с начальным сегментом 1, 2, 3, 4, 5, 6, 7, 8, является конечным множеством, содержащим 8 («восемь») элементов. Символ 8 указывает на «число» предметов в исходном множестве. Это число есть символ, или ярлык, приписываемый данному множеству. Этот же ярлык приписывается всем тем и только тем множествам, которые могут быть поставлены во взаимно однозначное соответствие с данным множеством. Однозначное определение ярлыка для любого заданного конечного множества называется «пересчитыванием» элементов данного множества, а сами ярлыки получили название натуральных или целых положительных чисел (см. также ЧИСЛО; МНОЖЕСТВ ТЕОРИЯ).

Пусть A и B – два конечных множества, не имеющие общих элементов, и пусть A содержит n элементов, а B содержит m элементов. Тогда множество S, состоящее из всех элементов множеств A и B, взятых вместе, является конечным множеством, содержащим, скажем, s элементов. Например, если А состоит из элементов {a, b, c}, множество В – из элементов {x, y}, то множество S = A + B и состоит из элементов {a, b, c, x, y}. Число s называется суммой чисел n и m, и мы записываем это так: s = n + m. В этой записи числа n и m называются слагаемыми, операция нахождения суммы – сложением. Символ операции «+» читается как «плюс». Множество P, состоящее из всех упорядоченных пар, в которых первый элемент выбран из множества A, а второй – из множества B, является конечным множеством, содержащим, скажем, p элементов. Например, если, как и прежде, A = {a, b, c}, B = {x, y}, то P = AґB = {(a,x), (a,y), (b,x), (b,y), (c,x), (c,y)}. Число p называется произведением чисел a и b, и мы записываем это так: p = aґb или p = aЧb. Числа a и b в произведении называются множителями, операция нахождения произведения – умножением. Символ операции ґ читается как «умноженное на».

Можно показать, что из этих определений следуют приводимые ниже фундаментальные законы сложения и умножения целых чисел:

– закон коммутативности сложения: a + b = b + a;

– закон ассоциативности сложения: a + (b + c) = (a + b) + c;

– закон коммутативности умножения: aґb = bґa;

– закон ассоциативности умножения: aґ(bґc) = (aґb)ґc;

– закон дистрибутивности: aґ(b + c)= (aґb) + (aґc).

Если a и b – два положительных целых числа и если существует положительное целое число c, такое, что a = b + c, то мы говорим, что a больше b (это записывается так: a > b), или что b меньше a (это записывается так: b < a). Для любых двух чисел a и b выполняется одно из трех соотношений: либо a = b, либо a > b, либо a < b.

Первые два фундаментальных закона говорят о том, что сумма двух или большего числа слагаемых не зависит от того, как они сгруппированы и в каком порядке они расположены. Аналогично, из третьего и четвертого законов следует, что произведение двух или большего числа множителей не зависит от того, как сгруппированы множители и каков их порядок. Эти факты известны как «обобщенные законы коммутативности и ассоциативности» сложения и умножения. Из них следует, что при написании суммы нескольких слагаемых или произведения нескольких множителей порядок слагаемых и множителей несуществен и можно опустить скобки.

В частности, повторная сумма a + a + ... + a из n слагаемых равна nґa. Повторное произведение aґaґ ... ґa из n множителей условились обозначать aⁿ; число a называется основанием, а число n – показателем повторного произведения, само повторное произведение – n-й степенью числа a. Эти определения позволяют установить следующие фундаментальные законы для показателей степени:

Еще одно важное следствие из определений: aґ1 = a для любого целого числа a, причем 1 – единственное целое число, обладающее этим свойством. Число 1 называется единицей.

Делители целых чисел.

Если a, b, c – целые числа и aґb = c, то a и b являются делителями числа c. Так как aґ1 = a для любого целого числа a, мы заключаем, что 1 – делитель любого целого числа и что любое целое число есть делитель самого себя. Любой делитель целого числа a, отличный от 1 или a, получил название собственного делителя числа a.

Любое целое число, отличное от 1 и не имеющее собственных делителей, называется простым числом. (Примером простого числа может служить число 7.) Целое число, имеющее собственные делители, называется составным числом. (Например, число 6 составное, так как 2 делит 6.) Из сказанного следует, что множество всех целых чисел подразделяется на три класса: единица, простые числа и составные числа.

В теории чисел есть очень важная теорема, которая утверждает, что «любое целое число может быть представлено в виде произведения простых чисел, и с точностью до порядка множителей такое представление единственно». Эта теорема известна как «основная теорема арифметики». Она показывает, что простые числа служат теми «кирпичиками», из которых с помощью умножения можно построить все целые числа, отличные от единицы.

Если задано некоторое множество целых чисел, то наибольшее целое число, которое является делителем каждого числа, входящего в это множество, называется наибольшим общим делителем данного множества чисел; наименьшее целое число, делителем которого служит каждое число из данного множества, называется наименьшим общим кратным данного множества чисел. Так, наибольший общий делитель чисел 12, 18 и 30 равен 6. Наименьшее общее кратное тех же самых чисел равно 180. Если наибольший общий делитель двух целых чисел a и b равен 1, то числа a и b называются взаимно простыми. Например, числа 8 и 9 – взаимно простые, хотя ни одно из них не является простым.

Положительные рациональные числа.

Как мы видели, целые числа являются абстракциями, возникающими из процесса пересчета конечных наборов предметов. Однако для потребностей повседневной жизни целых чисел оказывается недостаточно. Например, при измерении длины крышки стола принятая единица измерения может оказаться слишком большой и не укладываться целое число раз в измеряемой длине. Чтобы справиться с подобной трудностью, с помощью т.н. дробных (т.е., буквально, «поломанных») чисел вводится меньшая единица длины. Если d – некоторое целое число, то дробная единица 1/d определяется свойством dґ1/d = 1, и если n – целое число, то nґ1/d мы записываем просто как n/d. Такие новые числа получили название «обыкновенных» или «простых» дробей. Целое число n называется числителем дроби, а число d – знаменателем. Знаменатель показывает, на сколько равных долей разделили единицу, а числитель показывает, сколько таких долей взяли. Если n < d, дробь называется правильной; если же n = d или n > d, то – неправильной. Целые числа рассматриваются как дроби с знаменателем, равным 1; например, 2 = 2/1.

Так как дробь n/d можно интерпретировать как результат деления n единиц на d равных долей и взятия одной из таких долей, дробь можно рассматривать как «частное» или «отношение» двух целых чисел n и d, а черту дроби понимать как знак деления. Поэтому дроби (в т.ч. и целые числа как частный случай дробей) обычно называют рациональными числами (от лат. ratio – отношение).

Две дроби n/d и (kґn)/(kґd), где k – целое число, можно рассматривать как равные; например, 4/6 = 2/3. (Здесь n = 2, d = 3 и k = 2.) Это обстоятельство известно как «основное свойство дроби»: значение любой дроби не изменится, если числитель и знаменатель дроби умножить (или разделить) на одно и то же число. Отсюда следует, что любую дробь можно записать как отношение двух взаимно простых чисел.

Из предложенной выше интерпретации дроби также следует, что в качестве суммы двух дробей n/d и m/d, имеющих один и тот же знаменатель, следует принять дробь (n + m)/d. При сложении дробей с разными знаменателями нужно сначала преобразовать их, пользуясь основным свойством дроби, в эквивалентные дроби с одинаковым (общим) знаменателем. Например, n₁/d₁ = (n₁Чd₂)/(d₁Чd₂) и n₂/d₂ = (n₂Чd₁)/(d₁Чd₂), откуда

Можно было бы поступить иначе и сначала найти наименьшее общее кратное, скажем, m, знаменателей d₁ и d₂. Тогда существуют целые числа k₁ и k₂, такие, что m = k₁Чd₁ = k₂Чd₂, и мы получаем:

откуда

При таком способе число m обычно называется наименьшим общим знаменателем двух дробей. Эти два результата эквивалентны по определению равенства дробей.

Произведение двух дробей n₁/d₁ и n₂/d₂ принимается равным дроби (n₁Чn₂)/(d₁Чd₂).

Восемь фундаментальных законов, приведенных выше для целых чисел, справедливы и в том случае, если под a, b, c понимать произвольные положительные рациональные числа. Кроме того, если даны два положительных рациональных числа n₁/d₁ и n₂/d₂, то мы говорим, что n₁/d₁ > n₂/d₂ тогда и только тогда, когда n₁Чd₂ > n₂Чd₁.

Положительные действительные числа.

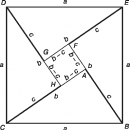
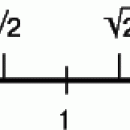
Применение чисел для измерения длин отрезков прямых наводит на мысль, что для любых двух данных отрезков прямых AB и CD должен существовать некоторый отрезок UV, возможно, очень малый, который можно было бы отложить целое число раз в каждом из отрезков AB и CD. Если такая общая единица измерения длины UV существует, то отрезки AB и CD называются соизмеримыми. Уже в древности пифагорейцы знали о существовании несоизмеримых отрезков прямых. Классический пример – сторона квадрата и его диагональ. Если принять сторону квадрата за единицу длины, то не найдется такого рационального числа, которое могло бы быть мерой диагонали этого квадрата. Убедиться в этом можно, рассуждая от противного. Действительно, предположим, что рациональное число n/d есть мера диагонали. Но тогда отрезок 1/d можно было бы отложить n раз на диагонали и d раз на стороне квадрата вопреки тому, что диагональ и сторона квадрата несоизмеримы. Следовательно, независимо от выбора единицы длины не все отрезки прямых имеют длины, выражаемые рациональными числами. Чтобы все отрезки прямой можно было измерять с помощью некоторой единицы длины, система счисления должна быть расширена таким образом, чтобы она включала числа, представляющие результаты измерения длин отрезков прямых, несоизмеримых с выбранной единицей длины. Эти новые числа называются положительными иррациональными числами. Последние вместе с положительными рациональными числами образуют более широкое множество чисел, элементы которого называются положительными действительными числами.

Если OR – горизонтальная полупрямая, исходящая из точки O, U – точка на OR, отличная от начала координат O, и OU выбран в качестве единичного отрезка, то каждой точке P на полупрямой OR можно поставить в соответствие единственное положительное действительное число p, выражающее длину отрезка OP. Таким образом мы устанавливаем взаимно однозначное соответствие между положительными действительными числами и точками, отличными от O, на полупрямой OR. Если p и q – два положительных действительных числа, соответствующих точкам P и Q на OR, то мы пишем p > q, p = q или p < q в зависимости от того, расположена точка P справа от точки Q на OR, совпадает с Q или расположена слева от Q.

Введение положительных иррациональных чисел существенно расширило сферу применимости арифметики. Например, если a – любое положительное действительное число и n – любое целое число, то существует единственное положительное действительное число b, такое, что bⁿ = a. Это число b называется корнем n-й степени из a и записывается как , где символ по своим очертаниям напоминает латинскую букву r, с которой начинается латинское слово radix (корень) и называется радикалом. Можно показать, что

Эти соотношения известны как основные свойства радикалов.

С практической точки зрения очень важно, что любое положительное иррациональное число можно сколь угодно точно аппроксимировать положительным рациональным числом. Это означает, что если r – положительное иррациональное число и e – сколь угодно малое положительное рациональное число, то можно найти положительные рациональные числа a и b, такие, что a < r < b и b < a + e. Например, число иррационально. Если выбрать e = 0,01, то ; если же выбрать e = 0,001, то .

Индо-арабская система счисления.

Алгоритмы, или схемы вычислений, арифметики зависят от используемой системы счисления. Совершенно очевидно, например, что методы вычислений, придуманные для римской системы счисления, могут отличаться от алгоритмов, изобретенных для действующей ныне индо-арабской системы. Более того, некоторые системы счисления могут оказаться совсем неподходящими для построения арифметических алгоритмов. Исторические данные свидетельствуют, что до принятия индо-арабской системы обозначения чисел вообще не существовало каких-либо алгоритмов, позволявших достаточно легко с помощью «карандаша и бумаги» выполнять сложение, вычитание, умножение и деление чисел. За долгие годы существования индо-арабской системы были разработаны специально к ней приспособленные многочисленные алгоритмические процедуры, так что наши современные алгоритмы являются продуктом целой эпохи развития и усовершенствования (см. также ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ).

В индо-арабской системе счисления каждая запись, обозначающая число, представляет собой набор из десяти основных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемых цифрами. Например, индо-арабское обозначение числа четыреста двадцать три имеет вид последовательности цифр 423. Значение цифры в индо-арабской записи числа определяется ее местом, или позицией, в последовательности цифр, образующих эту запись. В приведенном нами примере цифра 4 означает четыре сотни, цифра 2 – два десятка и цифра 3 – три единицы. Очень важную роль играет цифра 0 (нуль), используемая для заполнения пустых позиций; например, запись 403 означает число четыреста три, т.е. отсутствуют десятки. Если a, b, c, d, e означают отдельные цифры, то в индо-арабской системе abcde означает сокращенную запись целого числа

Так как каждое целое число допускает единственное представление в виде

где n – целое число, а a₀, a₁,..., a_n – цифры, мы заключаем, что в данной системе счисления каждое целое число можно представить единственным способом.

Индо-арабская система счисления позволяет сжато записывать не только целые, но и любые положительные действительные числа. Введем обозначение 10^-n для 1/10ⁿ, где n – произвольное положительное целое число. Тогда, как можно показать, любое положительное действительное число представимо, причем единственным образом, в виде

Эту запись можно сжать, записав в виде последовательности цифр

где знак, называемый десятичной запятой, между a₀ и b₁ указывает, где начинаются отрицательные степени числа 10 (в некоторых странах с этой целью используется точка). Такой способ записи положительного действительного числа получил название десятичного разложения, а дробь, представленная в виде своего десятичного разложения, – десятичной.

Можно показать, что для положительного рационального числа десятичное разложение после запятой либо обрывается (например, 7/4 = 1,75), либо повторяется (например, 6577/1980 = 3,32171717...). Если число иррационально, то его десятичное разложение не обрывается и не повторяется. Если десятичное разложение иррационального числа на каком-то знаке после запятой оборвать, мы получим его рациональное приближение. Чем дальше справа от запятой расположен знак, на котором мы обрываем десятичное разложение, тем лучше рациональное приближение (тем меньше ошибка).

В индо-арабской системе число записывается с помощью десяти основных цифр, значение которых зависит от их места, или позиции, в записи числа (значение цифры равно произведению цифры на некоторую степень числа 10). Поэтому такая система называется десятичной позиционной системой. Позиционные системы счисления очень удобны для построения арифметических алгоритмов, и именно этим объясняется столь широкое распространение индо-арабской системы счисления в современном мире, хотя в разных странах для обозначения отдельных цифр могут использоваться разные символы.

Названия чисел.

Названия чисел в индо-арабской системе строятся по определенным правилам. Наиболее употребительный способ наименования чисел заключается в том, что число прежде всего делят на группы из трех цифр справа налево. Эти группы называются «периодами». Первый период называется периодом «единиц», второй – периодом «тысяч», третий – периодом «миллионов» и т.д., как показано на следующем примере:

Каждый период читается так, как если бы он был трехзначным числом. Например, период 962 читается как «девятьсот шестьдесят два». Чтобы прочитать число, состоящее из нескольких периодов, прочитывается группа цифр в каждом периоде, начиная с самого левого и далее по порядку слева направо; после каждой группы следует название периода. Например, приведенное выше число читается как «семьдесят три триллиона восемьсот сорок два миллиарда девятьсот шестьдесят два миллиона пятьсот тридцать две тысячи семьсот девяносто восемь». Обратите внимание на то, что при чтении и записи целых чисел союз «и» обычно не используется. Название разряда единиц опускается. За триллионами следуют квадриллионы, квинтиллионы, секстиллионы, септиллионы, октиллионы, ноналлионы, дециллионы. Каждый период имеет значение, в 1000 раз превышающее значение предыдущего.

В индо-арабской системе принято придерживаться следующей процедуры чтения цифр, стоящих справа от десятичной запятой. Здесь позиции называются (по порядку слева направо): «десятые», «сотые», «тысячные», «десятитысячные» и т.д. Правильная десятичная дробь читается так, как если бы цифры после десятичной запятой образовывали целое число, после чего добавляется название позиции последней справа цифры. Например, 0,752 читается как «семьсот пятьдесят две тысячных». Смешанное десятичное число читается путем объединения правила наименования целых чисел с правилом наименования правильных десятичных дробей. Например, 632,752 читается как «шестьсот тридцать две целых семьсот пятьдесят две тысячных». Обратите внимание на слово «целых», произносимое перед десятичной запятой. В последние годы десятичные числа все чаще читают более просто, например, 3,782 как «три запятая семьсот восемьдесят два».

Сложение.

Теперь мы уже готовы к тому, чтобы проанализировать арифметические алгоритмы, с которыми знакомят в начальной школе. Эти алгоритмы относятся к действиям над положительными действительными числами, записанными в виде десятичных разложений. Мы предполагаем, что элементарные таблицы сложения и умножения выучены наизусть.

Рассмотрим задачу на сложение: вычислить 279,8 + 5,632 + 27,54:

Сначала мы суммируем одинаковые степени числа 10. Число 19Ч10^–1 разбивается по дистрибутивному закону на 9Ч10^–1 и 10Ч10^–1 = 1. Единицу мы переносим влево и прибавляем к 21, что дает 22. В свою очередь, число 22 мы разбиваем на 2 и 20 = 2Ч10. Число 2Ч10 переносим влево и прибавляем к 9Ч10, что дает 11Ч10. Наконец, 11Ч10 разбиваем на 1Ч10 и 10Ч10 = 1Ч10², 1Ч10² переносим влево и прибавляем к 2Ч10², что дает 3Ч10². Окончательная сумма оказывается равной 312,972.

Ясно, что проделанные вычисления можно представить в более сжатой форме, заодно использовав ее как пример алгоритма сложения, которому учат в школе. Для этого все три числа мы выписываем одно под другим так, чтобы десятичные запятые оказались на одной вертикали:

Начав справа, находим, что сумма коэффициентов при 10^–3 равна 2, что и записываем в соответствующем столбце под чертой. Сумма коэффициентов при 10^–2 равна 7, что также записываем в соответствующем столбце под чертой. Сумма коэффициентов при 10^–1 равна 19. Число 9 мы записываем под чертой, а 1 переносим в предыдущий столбец, где стоят единицы. С учетом этой единицы сумма коэффициента в этом столбце оказывается равной 22. Мы записываем одну двойку под чертой, а другую переносим в предыдущий столбец, где стоят десятки. С учетом перенесенной двойки сумма коэффициентов в этом столбце равна 11. Одну единицу мы записываем под чертой, а другую переносим в предыдущий столбец, где стоят сотни. Сумма коэффициентов в этом столбце оказывается равной 3, что и записываем под чертой. Требуемая сумма равна 312,972.

Вычитание.

Вычитание – это действие, обратное сложению. Если три положительных действительных числа a, b, c связаны между собой так, что a + b = c, то мы записываем a = c – b, где символ «-» читается как «минус». Нахождение числа a по известным числам b и c называется «вычитанием». Число c называется уменьшаемым, число b – «вычитаемым», а число a – «разностью». Поскольку мы имеем дело с положительными действительными числами, должно выполняться условие c > b.

Рассмотрим пример на вычитание: вычислить 453,87 – 82,94.

или

Прежде всего, заимствуя в случае необходимости единицу слева, мы преобразуем разложение уменьшаемого так, чтобы его коэффициент при любой степени числа 10 был больше коэффициента вычитаемого при той же степени. Из 4Ч10² мы заимствуем 1Ч10² = 10Ч10, прибавляя последнее число к следующему члену разложения, что дает 15Ч10; аналогично мы заимствуем 1Ч10⁰, или 10Ч10^–1, и прибавляем это число к предпоследнему члену разложения. После этого мы получаем возможность произвести вычитание коэффициентов при одинаковых степенях числа 10 и без труда находим разность 370,93.

Запись операций вычитания можно представить в более сжатом виде и получить пример алгоритма вычитания, изучаемого в школе. Запишем вычитаемое под уменьшаемым так, чтобы их десятичные запятые оказались на одной вертикали. Начав справа, найдем, что разность коэффициентов при 10^–2 равна 3, и это число запишем в том же столбце под чертой. Так как в следующем столбце слева мы не можем вычесть 9 из 8, мы изменяем тройку в положении единиц уменьшаемого на двойку и рассматриваем число 8 в позиции десятых как 18. После вычитания 9 из 18 мы получаем 9 и т.д., т.е.

Умножение.

Рассмотрим сначала т.н. «короткое» умножение – умножение положительного действительного числа на одно из однозначных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, например, 32,67ґ4. Пользуясь законом дистрибутивности, а также законами ассоциативности и коммутативности умножения, мы получаем возможность разбивать множители на части и располагать их более удобным образом. Например,

Эти вычисления можно записать более компактно следующим образом:

Процесс сжатия можно продолжить. Запишем множитель 4 под множимым 32,67, как указано:

Так как 4ґ7 = 28, мы записываем под чертой цифру 8, а 2 помещаем над цифрой 6 множимого. Далее, 4ґ6 = 24, что с учетом перенесенной из столбца справа дает 26. Цифру 6 мы записываем под чертой, а 2 записываем над цифрой 2 множимого. Затем мы получаем 4ґ2 = 8, что в сочетании с перенесенной двойкой дает 10. Цифру 0 мы подписываем под чертой, а единицу – над цифрой 3 множимого. Наконец, 4ґ3 = 12, что с учетом перенесенной единицы дает 13; число 13 записываем под чертой. Поставив десятичную запятую, получаем ответ: произведение равно 130,68.

«Длинное» умножение – это просто неоднократно повторенное «короткое» умножение. Рассмотрим, например, умножение числа 32,67 на число 72,4. Расположим множитель под множимым, как указано:

Производя справа налево короткое умножение, мы получаем первое частное произведение 13,068, второе – 65,34 и третье – 2286,9. По закону дистрибутивности, произведение, которое требуется найти, есть сумма этих частных произведений, или 2365,308. В письменной записи десятичная запятая в частных произведениях опускается, но их нужно правильно располагать «ступеньками», чтобы затем просуммировать и получить полное произведение. Число знаков после десятичной запятой в произведении равно сумме числа знаков после запятых в множимом и множителе.

Деление.

Деление – операция, обратная умножению; подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание. Рассмотрим, например, такой вопрос: сколько раз 3 содержится в 14? Повторяя операцию вычитания 3 из 14, мы находим, что 3 «входит» в 14 четыре раза, и еще «остается» число 2, т.е.

Число 14 называется делимым, число 3 – делителем, число 4 – частным и число 2 – остатком. Словами получившееся соотношение можно выразить так:

делимое = (делитель ґ частное) + остаток,

где

0 Ј остаток < делитель.

Чтобы найти частное и остаток от деления 1400 на 3 с помощью многократного вычитания 3, потребовалось бы затратить немало времени и труда. Процедуру можно было бы существенно ускорить, если сначала вычитать из 1400 по 300, затем из остатка по 30 и, наконец, по 3. После четырехкратного вычитания 300 мы получили бы в остатке 200; после шестикратного вычитания из 200 числа 30 остаток оказался бы равным 20; наконец, после шестикратного вычитания из 20 числа 3 мы получим остаток 2. Следовательно,

Частное и остаток, которые требовалось найти, равны, соответственно, 466 и 2. Вычисления можно организовать и затем последовательно подвергнуть сжатию следующим образом:

Приведенные выше рассуждения применимы, если делимое и делитель – любые положительные действительные числа, выраженные в десятичной системе. Проиллюстрируем это на примере 817,65ё23,7.

Сначала делитель с помощью сдвига десятичной запятой необходимо превратить в целое число. При этом десятичная запятая делимого сдвигается на такое же число десятичных знаков. Делитель и делимое располагаются, как показано ниже:

Определим, сколько раз делитель содержится в трехзначном числе 817, первой части делимого, которую мы делим на делитель. Так как по оценкам он содержится три раза, мы умножаем 237 на 3 и произведение 711 вычитаем из 817. Разность 106 меньше делителя. Это означает, что число 237 входит в пробное делимое не более трех раз. Цифра 3, написанная под цифрой 2 делителя ниже горизонтальной черты, – первая цифра частного, которое требуется найти. После того, как мы снесем вниз следующую цифру делимого, получится следующее пробное делимое 1066, и надо определить, сколько раз делитель 237 укладывается в числе 1066; предположим, что 4 раза. Умножаем делитель на 4 и получаем произведение 948, которое вычитаем из 1066; разность оказывается равной 118, что означает, что следующая цифра частного равна 4. Затем мы сносим следующую цифру делимого и повторяем всю процедуру, описанную выше. На этот раз оказывается, что пробное делимое 1185 точно (без остатка) делится на 237 (остаток от деления наконец оказывается равным 0). Отделив десятичной запятой в частном столько же знаков, сколько их отделено в делимом (напомним, что ранее мы десятичную запятую переносили), получим ответ: частное равно 34,5.

Дроби.

Вычисления с дробями включают сложение, вычитание, умножение и деление, а также упрощение сложных дробей.

Сложение дробей с одним и тем же знаменателем производится путем сложения числителей, например,

1/16 + 5/16 + 7/16 = (1 + 5 + 7)/16 = 13/16.

Если дроби имеют различные знаменатели, то предварительно их необходимо привести к общему знаменателю, т.е. превратить в дроби с одинаковыми знаменателями. Для этого мы находим наименьший общий знаменатель (наименьшее число, кратное каждому из данных знаменателей). Например, при сложении 2/3, 1/6 и 3/5 наименьший общий знаменатель равен 30:

Суммируя, получаем

20/30 + 5/30 + 18/30 = 43/30.

Вычитание дробей производится так же, как их сложение. Если знаменатели одинаковы, то вычитание сводится к вычитанию числителей: 10/13 – 2/13 = 8/13; если дроби имеют различные знаменатели, то предварительно необходимо привести их к общему знаменателю:

7/8 – 3/4 = 7/8 – 6/8 = (7 – 6)/8 = 1/8.

При умножении дробей их числители и знаменатели умножаются отдельно. Например,

5/6ґ4/9 = 20/54 = 10/27.

Чтобы разделить одну дробь на другую, необходимо умножить первую дробь (делимое) на дробь, обратную второй (делителю) (чтобы получить обратную дробь, надо поменять местами числитель и знаменатель исходной дроби), т.е. (n₁/d₁)ё(n₂/d₂) = (n₁Чd₂)/(d₁Чn₂). Например,

3/4ё7/8 = 3/4ґ8/7 = 24/28 = 6/7.

Смешанное число представляет собой сумму (или разность) целого числа и дроби, например, 4 + 2/3 или 10 – 1/8. Так как целое число можно рассматривать как дробь с знаменателем, равным 1, смешанное число есть не что иное, как сумма (или разность) двух дробей. Например,

4 + 2/3 = 4/1 + 2/3 = 12/3 + 2/3 = 14/3.

Сложной называется дробь, имеющая дробь либо в числителе, либо в знаменателе, либо в числителе и знаменателе. Такую дробь можно превратить в простую:

Квадратный корень.

Если n – положительное действительное число, то существует единственное положительное действительное число r, такое, что r² = n. Число r называется квадратным корнем из n и обозначается . В школе учат извлекать квадратные корни двумя способами.

Первый способ более популярен, поскольку он проще и его легче применять; вычисления по этому методу легко реализуются на настольном калькуляторе и обобщаются на случай кубических корней и корней более высокой степени. Основан метод на том, что если r₁ – приближение к корню , то r₂ = (1/2)(r₁ + n/r₁) – более точная аппроксимация корня.

Проиллюстрируем процедуру на примере вычисления квадратного корня из какого-нибудь числа, заключенного между 1 и 100, скажем, числа 40. Так как 6² = 36, а 7² = 49, мы заключаем, что 6 – наилучшее приближение к в целых числах. Более точное приближение к получается из 6 следующим образом. Разделив 40 на 6, получим 6,6 (с округлением до первого после запятой четного числа десятых). Чтобы получить второе приближение к , усредним два числа 6 и 6,6 и получим 6,3. Повторив процедуру, получим еще лучшее приближение. Разделив 40 на 6,3, находим число 6,350, и третье приближение оказывается равным (1/2)(6,3 + 6,350) = 6,325. Еще одно повторение дает 40ё6,325 = 6,3241106, и четвертая аппроксимация оказывается равной (1/2)(6,325 + 6,3241106) = 6,3245553. Процесс может продолжаться сколь угодно долго. В общем случае каждое следующее приближение может содержать вдвое больше цифр, чем предыдущее. Так, в нашем примере, поскольку первое приближение, целое число 6, содержит только одну цифру, мы можем удерживать во втором приближении два знака, в третьем – четыре и в четвертом – восемь.

Если число n не лежит между 1 и 100, то следует предварительно разделить (или умножить) n на некоторую степень числа 100, скажем, на k-ю, чтобы произведение оказалось в интервале от 1 до 100. Тогда квадратный корень из произведения будет находиться в интервале от 1 до 10, и после того, как он будет извлечен, мы, умножив (или разделив) полученное число на 10^k, найдем искомый квадратный корень. Например, если n = 400000, то мы сначала делим 400000 на 100² и получаем число 40, лежащее в интервале от 1 до 100. Как показано выше, приближенно равен 6,3245553. Умножая это число на 10², получаем 632,45553 в качестве приближенного значения для , а число 0,63245553 служит приближенным значением для .

Вторая из упомянутых выше процедур основана на алгебраическом тождестве (a + b)² = a² + (2a + b)b. На каждом шаге уже полученная часть квадратного корня принимается за a, а часть, которую еще требуется определить, – за b.

Кубический корень.

Для извлечения кубического корня из положительного действительного числа существуют алгоритмы, аналогичные алгоритмам извлечения квадратного корня. Например, чтобы найти кубический корень из числа n, сначала мы аппроксимируем корень некоторым числом r₁. Затем строим более точное приближение r₂ = (1/3)(2r₁ + n/r₁²), которое в свою очередь уступает место еще более точному приближению r₃ = (1/3)(2r₂ + n/r₂²) и т.д. Процедура построения все более точных приближений корня может продолжаться сколь угодно долго.

Рассмотрим, например, вычисление кубического корня из числа, заключенного между 1 и 1000, скажем, числа 200. Так как 5³ = 125 и 6³ = 216, мы заключаем, что 6 – ближайшее к кубическому корню из 200 целое число. Следовательно, выбираем r₁ = 6 и последовательно вычисляем r₂ = 5,9, r₃ = 5,85, r₄ = 5,8480. В каждом приближении, начиная с третьего, разрешается удерживать число знаков, которое на единицу меньше удвоенного числа знаков в предыдущем приближении. Если же число, из которого требуется извлечь кубический корень, не заключено между 1 и 1000, то предварительно его необходимо разделить (или умножить) на некоторую, скажем, k-ю, степень числа 1000 и тем самым привести в нужный интервал чисел. Кубический корень из вновь полученного числа лежит в интервале от 1 до 10. После того, как он будет вычислен, его необходимо умножить (или разделить) на 10^k, чтобы получить кубический корень из исходного числа.

Второй, более сложный, алгоритм нахождения кубического корня из положительного действительного числа основан на использовании алгебраического тождества (a + b)³ = a³ + (3a² + 3ab + b²)b. В настоящее время алгоритмы извлечения кубических корней, равно как и корней более высоких степеней, в средней школе не изучают, так как их легче находить с помощью логарифмов или алгебраическими методами.

Алгоритм Евклида.

Этот алгоритм был изложен в Началах Евклида (ок. 300 до н.э.). С его помощью вычисляется наибольший общий делитель двух целых чисел. Для случая положительных чисел он формулируется в виде процедурного правила: «Разделите большее из двух данных чисел на меньшее. Затем разделите делитель на остаток от деления и продолжайте действовать так же, пока последний делитель не разделится нацело на последний остаток. Последний из делителей и будет наибольшим общим делителем двух данных чисел».

В качестве числового примера рассмотрим два целых числа 3132 и 7200. Алгоритм в этом случае сводится к следующим действиям:

Наибольший общий делитель совпадает с последним делителем – числом 36. Объяснение просто. В нашем примере мы видим из последней строки, что число 36 делит число 288. Из предпоследней строки следует, что число 36 делит 324. Так, двигаясь от строки к строке вверх, мы убеждаемся в том, что число 36 делит 936, 3132 и 7200. Мы утверждаем теперь, что число 36 есть общий делитель чисел 3132 и 7200. Пусть g – наибольший общий делитель чисел 3132 и 7200. Так как g делит 3132 и 7200, из первой строки следует, что g делит 936. Из второй строки мы заключаем, что g делит 324. Так, спускаясь от строки к строке, мы убеждаемся в том, что g делит 288 и 36. А так как 36 – общий делитель чисел 3132 и 7200 и делится на наибольший общий их делитель, мы заключаем, что 36 и есть этот наибольший общий делитель.

Проверка.

Арифметические вычисления требуют постоянного внимания и, следовательно, чреваты ошибками. Поэтому очень важно проверять результаты вычислений.

1. Сложение столбца чисел можно проверить, сложив числа в столбце сначала сверху вниз, а затем снизу вверх. Обоснованием такого способа проверки служит обобщенный закон коммутативности и ассоциативности сложения.

2. Вычитание проверяется путем сложения разности с вычитаемым – должно получиться уменьшаемое. Обоснованием такого способа проверки служит определение операции вычитания.

3. Умножение можно проверить, переставив множимое и множитель. Обоснованием такого способа проверки служит закон коммутативности умножения. Можно проверить умножение, разбив множитель (или множимое) на два слагаемых, выполнив две отдельные операции умножения и сложив полученные произведения – должно получиться исходное произведение.

4. Чтобы проверить деление, надо умножить частное на делитель и к произведению прибавить остаток. Должно получиться делимое. Обоснованием такого способа проверки служит определение операции деления.

5. Проверка правильности извлечения квадратного (или кубического) корня состоит в возведении полученного числа в квадрат (или куб) – должно получиться исходное число.

Особенно простым и весьма надежным способом проверки сложения или умножения целых чисел служит прием, представляющий собой переход к т.н. «сравнениям по модулю 9». Назовем «избытком» остаток от деления на 9 суммы цифр, которыми записано данное число. Тогда относительно «избытков» можно сформулировать две теоремы: «избыток суммы целых чисел равен избытку суммы избытков слагаемых», и «избыток произведения двух целых чисел равен избытку произведения их избытков». Ниже даются примеры проверок, основанных на этой теореме:

Метод перехода к сравнениям по модулю 9 можно использовать и при проверке других арифметических алгоритмов. Конечно, и такая проверка не является непогрешимой, так как и работа с «избытками» подвержена ошибкам, но такая ситуация маловероятна.

Проценты.

Процентом называется дробь, у которой знаменатель равен 100; проценты можно записать тремя способами: как обыкновенную дробь, как десятичную дробь или с помощью специального обозначения процентов %. Например, 7 процентов можно записать как 7/100, как 0,07 или как 7%.

Примером самого распространенного типа задач на проценты может служить следующая: «Найти 17% от 82». Чтобы решить эту задачу, нужно вычислить произведение 0,17ґ82 = 13,94. В произведениях такого рода 0,17 называется ставкой, 82 – базой, а 13,94 – долей, выраженной в процентах. Три упомянутые величины связаны между собой соотношением

Ставка ґ база = доля в процентах.

Если любые две величины известны, третью можно определить из этого соотношения. Соответственно мы получаем три типа задач «на проценты».

Пример 1. Число учащихся, записавшихся в данную школу, выросло с 351 до 396 человек. На сколько процентов возросло это число?

Прирост составил 396 – 351 = 45 человек. Записывая дробь 45/351 в процентах, получаем 45/351 = 0,128 = 12,8%.

Пример 2. Объявление в магазине во время распродажи гласит «Скидка на все товары 25%». Какова цена во время распродажи на товар, который обычно продается за 3,60 доллара?

Снижение цены 3,60 доллара на 25% означает снижение на 0,25ґ3,60 = 0,90 доллара; следовательно, цена на товар во время распродажи составит 3,60 – 0,90 = 2,70 доллара.

Пример 3. Деньги, положенные в банк под 5% годовых, принесли прибыль в 40 долларов за год. Какая сумма была помещена в банк?

Так как 5% от суммы составляет 40 долларов, т.е. 5/100 ґ сумма = 40 долларов, или 1/100 ґ сумма = 8 долларов, вся сумма составляет 800 долларов.

Арифметика приближенных чисел.

Многие числа, используемые в вычислениях, возникают либо из измерений, либо из оценок и поэтому могут рассматриваться лишь как приближенные. Очевидно, что результатом вычислений, производимых с приближенными числами, может быть только приближенное число. Например, предположим, что измерения поверхности прилавка дали следующие результаты (с округлением до ближайшей десятой метра): ширина 1,2 м, длина 3,1 м; можно было бы сказать, что площадь прилавка составляет 1,2ґ3,1 = 3,72 м². Однако в действительности информация далеко не столь определенна. Так как величина 1,2 м указывает лишь на то, что результат измерения ширины заключен между 1,15 и 1,25 м, а 3,1 – на то, что результат измерения длины заключен между 3,05 и 3,15 м, о площади прилавка можно лишь сказать, что она должна быть больше, чем 1,15ґ3,05 = 3,5075, но меньше, чем 1,25ґ3,15 = 3,9375. Следовательно, единственный разумный ответ на вопрос о площади прилавка состоит в утверждении, что она приблизительно равна 3,7 м².

Рассмотрим далее проблему сложения результатов приближенных измерений 3,73 м, 52,1 м и 0,282 м. Простая сумма равна 56,112 м. Но, как и в предыдущей задаче, все, что можно сказать с уверенностью, так это то, что истинная сумма должна быть больше, чем 3,725 + 52,05 + 0,2815 = 56,0565 м и меньше, чем 3,735 + 52,15 + 0,2825 = 56,1765 м. Таким образом, единственный разумный ответ на вопрос сводится к утверждению, что сумма приближенно равна 56,1 м.

Два приведенных выше примера иллюстрируют некоторые правила, полезные при работе с приближенными числами. Существуют различные способы округления чисел. Один из них состоит в отбрасывании младших разрядов числа. При этом если первая отбрасываемая цифра больше пяти, то последний оставшийся знак надо увеличить на единицу, если меньше, то последний знак оставляемой части сохраняется неизменным.

Если же первая отбрасываемая цифра в точности равна пяти, то последняя сохраняемая цифра увеличивается на единицу, если она нечетная, и остается без изменений, если она четная. Например, при округлении до сотых числа 3,14159;17,7682; 28,999; 0,00234; 7,235 и 7,325 переходят в числа 3,14; 17,77; 29,00; 0,00; 7,24 и 7,32.

Другой способ округления связан с понятием значащих цифр и используется при машинной записи числа. Значащими цифрами приближенного числа называются цифры в его десятичной записи по порядку слева направо, начиная с первой отличной от нуля цифры и кончая той цифрой, которая стоит на месте десятичного знака, соответствующего ошибке. Например, значащими цифрами приближенного числа 12,1 являются цифры 1, 2, 1; приближенного числа 0,072 – цифры 7, 2; приближенного числа 82000, записанного с точностью до сотен, – 8, 2, 0.

Теперь мы сформулируем два упоминавшихся выше правила действий с приближенными числами.

При сложении и вычитании приближенных чисел округлять каждое число следует до знака, следующего по номеру за последним знаком наименее точного числа, а полученную сумму и разность округлять до такого же количества знаков, как у наименее точного числа. При умножении и делении приближенных чисел каждое число следует округлять до знака, следующего по номеру за последней значащей цифрой наименее значащего числа, а произведение и частное округлять с той же точностью, с какой известно наименее точное число.

Возвращаясь к ранее рассмотренным задачам, получаем:

1,2ґ3,1 = 3,72 м² » 3,7 м²

и

3,73 + 52,1 + 0,28 = 56,11 м² » 56,1 м,

где знак » означает «приближенно равно».

В некоторых учебниках арифметики приводятся алгоритмы для работы с приближенными числами, позволяющие избегать при вычислениях лишних знаков. Кроме того, в них используется т.н. запись приближенных чисел, т.е. любое число представляется в виде (число, заключенное в интервале от 1 до 10) ґ (степень числа 10), где в первом множителе содержатся только значащие цифры числа. Например, 82000 км, округленные до ближайшего числа сотен км, запишется как 8,20ґ10⁴ км, а 0,00702 см – как 7,02ґ10^–3 см.

Числа в математических таблицах, тригонометрических или таблицах логарифмах, – приближенные, записанные с определенным числом знаков. При работе с такими таблицами следует придерживаться правил для вычислений с приближенными числами.

Логарифмы.

К началу 17 в. сложность прикладных вычислительных задач возросла настолько, что справиться с ними «вручную» не представлялось возможным из-за слишком больших затрат труда и времени. К счастью, вовремя изобретенные Дж.Непером в начале 17 в. логарифмы позволили справиться с возникшей было проблемой. Так как теория и приложения логарифмов подробно изложены в специальной статье ЛОГАРИФМ, мы ограничимся лишь самыми необходимыми сведениями.

Можно показать, что если n – положительное действительное число, то существует единственное положительное действительное число x, такое, что 10^x = n. Число x называется (обычным или десятичным) логарифмом числа n; условно это записывается так: x = log n. Таким образом, логарифм – это показатель степени, и из законов действий с показателями следует, что

Именно этими свойствами логарифмов объясняется их широкое использование в арифметике. Первое и второе свойства позволяют свести любую задачу на умножение и деление к более простой задаче на сложение и вычитание. Третье и четвертое свойства дают возможность свести возведение в степень и извлечение корня к гораздо более простым действием: умножению и делению.

Для удобства использования логарифмов были составлены их таблицы. Для составления таблицы десятичных логарифмов достаточно включить в них только логарифмы чисел от 1 до 10. Например, так как 247,6 = 10²ґ2,476, имеем: log247,6 = log10² + log2,476 = 2 + log2,476, а так как 0,02476 = 10^–2ґ2,476, то log0,02476 = log10^–2 + log2,476 = –2 + log2,476. Заметим, что десятичный логарифм числа, заключенного в интервале от 1 до 10, лежит в интервале от 0 до 1 и может быть записан в виде десятичной дроби. Отсюда следует, что десятичный логарифм любого числа есть сумма целого числа, называемого характеристикой логарифма, и десятичной дроби, называемой мантиссой логарифма. Характеристику логарифма любого числа можно найти «в уме»; мантиссу же следует находить по таблицам логарифмов. Например, из таблиц мы находим, что log2,476 = 0,39375, откуда log247,63 = 2,39375. Если характеристика логарифма отрицательна (когда число меньше единицы), то ее удобно представить в виде разности двух положительных целых чисел, например, log0,02476 = –2 + 0,39375 = 8,39375 – 10. Следующие примеры поясняют этот прием.

Чтобы найти произведение

x = 41,639ґ159,28ґ0,0037456,

мы по пятизначным таблицам логарифмов находим нужные мантиссы 0,61950; 0,20216 и 0,57352. Соответственно, логарифмы множителей равны

Складывая их, получаем

Еще один пример. Чтобы найти , мы находим, что log0,68317 = 9,83453 – 10. Так как для нахождения кубического корня, необходимо разделить полученное значение логарифма на 3, удобнее представить логарифм в виде 29,83453 – 30. Тогда log x = (1/3)log0,68317 = 9,94484 – 10; x = 0,88072.

Так как log n в общем случае – число иррациональное, в таблицах приводятся значения логарифмов с определенным числом десятичных знаков, и можно выбрать те из них, которые лучше всего соответствуют решаемой задаче. До появления современных компьютеров практически все длинные и сложные вычисления выполнялись с помощью таблиц логарифмов.