МОМЕНТЫ АТОМОВ И ЯДЕР
МОМЕНТЫ АТОМОВ И ЯДЕР. Термин «момент» применительно к атомам и атомным ядрам может означать следующее: 1) спиновый момент, или спин, 2) магнитный дипольный момент, 3) электрический квадрупольный момент, 4) прочие электрические и магнитные моменты. Различные типы моментов по отдельности рассматриваются ниже.
Существование у атома момента импульса и магнитного момента следовало из теории Н.Бора (1913) и подтверждалось обнаруженным еще в 1896 П.Зееманом влиянием магнитных полей на спектральные линии атома. Прямое измерение относительного магнитного момента атома было выполнено впервые в 1922 О.Штерном и В.Герлахом, которые наблюдали расщепление пучка атомов серебра в неоднородном магнитном поле. Первым предположение о существовании спина и магнитного момента у атомного ядра высказал в 1924 В.Паули при попытке объяснить сверхтонкую структуру спектральных линий. В 1925 Д.Уленбек и С.Гаудсмит на основе данных о тонкой структуре спектральных линий сделали вывод о том, что у электрона должны существовать спин и магнитный момент. Первое доказательство существования у ядра электрического квадрупольного момента было получено Х.Шюлером и Т.Шмидтом в 1935. Многочисленные измерения ядерных моментов были выполнены О.Штерном и И.Раби с сотрудниками, исследовавшими спектральные линии методом молекулярных пучков. Затем в 1937 и 1946 эти измерения продолжили И.Раби, Н.Рамзей, Э.Парселл, Ф.Блох и другие исследователи с помощью разработанных ими методов радиочастотного резонанса, потом – парамагнитного резонанса, а еще позднее – методами микроволновой и лазерной спектроскопии.
Спин.
Любое вращающееся тело обладает моментом импульса относительно своего центра масс; это собственный момент тела, или спин. Спиновый момент, или просто, спин атома или атомного ядра является характеристикой, аналогичной моменту импульса вращающегося волчка или гироскопа. Момент импульса твердого тела, вращающегося вокруг оси, определяется как сумма моментов импульсов всех частиц этого тела относительно той же оси; этот момент равен сумме произведений массы частицы на ее скорость и на кратчайшее расстояние частицы до оси вращения. Вектор момента импульса параллелен оси вращения и направлен в сторону перемещения винта с правой резьбой при таком же вращении. Спин атомов и ядер измеряется в единицах h/2p, где h – постоянная Планка, равная 6,6261Ч10–34 ДжЧс. Экспериментально установлено, что в этих единицах (в соответствии с правилами квантовой механики) наблюдаемые проекции всех спинов на заданное направление принимают либо целое, либо полуцелое значение, т.е. либо 1, 2, 3,..., либо 1/2, 3/2, 5/2,.... Максимальное значение проекции совпадает с величиной спина; например, если спин ядра j равен 5/2, то измеренное максимальное значение проекции спина составит 5/2 в единицах h/2p ДжЧс.
Магнитный дипольный момент.
Магнитный дипольный момент атома или ядра аналогичен характеристике стрелки компаса. Он представляет собой вращающий момент, действующий на атом или ядро в магнитном поле. Дипольный момент – векторная величина. Магнитный момент атома обычно измеряют в единицах магнетона Бора, m0 = еh/4pmc = 9,27Ч10–24 Дж/Тл, где е – заряд электрона, h – постоянная Планка, m – масса электрона и c – скорость света. Магнитные же моменты ядер обычно измеряют в единицах ядерного магнетона mN, который равен магнетону Бора, деленному на отношение масс протона и электрона, а именно mN = 5,051Ч10–27 Дж/Тл.
Электрический квадрупольный момент.
Электрический квадрупольный момент служит мерой отклонения распределения электрического заряда ядра от сферической симметрии. Количественно он определяется как 
при условии, что проекция спина ядра максимальна вдоль оси z прямоугольной системы координат, начало которой совпадает с центром ядра. В этом выражении Z – заряд ядра, или его атомный номер, z – координата протона в ядре, r – расстояние от протона до центра ядра, а черта над выражением в скобках означает усреднение плотности заряда по всему ядру. Можно показать, что в сферически симметричном случае Q = 0.
Другие моменты.
В принципе могли бы существовать электрические и магнитные мультипольные моменты любого порядка 2n, где n – нуль или положительное целое число. Например, у ядер иода, индия и галлия были измерены магнитные октуполи. Можно показать, однако, что вследствие квантовой природы спина атом или ядро со спином j не может иметь мультипольных моментов более высокого порядка, чем n = 2j. Так, атом с j = l/2 не может иметь мультипольных моментов выше дипольного, а атом с j = 0 – даже дипольного момента. Проводились необычайно чувствительные эксперименты по обнаружению у ядер электрических дипольных моментов, но пока что найти их не удалось.
АТОМНЫЕ МОМЕНТЫ
Эффект Зеемана.
Один из первых и наиболее мощных методов исследования атомных моментов был основан на так называемом эффекте П.Зеемана, т.е. на расщеплении спектральных линий во внешних магнитных полях. Если разрядную трубку, в которой возбуждается атомное излучение, поместить во внешнее магнитное поле, то спектральные линии расщепятся на ряд компонент. Расстояние между линиями компонент определяется энергией взаимодействия атомных моментов с внешними магнитными полями. Поскольку энергия взаимодействия зависит от магнитных моментов атомов, измеренное расщепление дает информацию об их величине. Числом спектральных линий определяются значения спина.
Первоначально при изучении оптических спектров атомов последние возбуждались за счет столкновений с электронами в газоразрядных трубках или за счет поглощения электромагнитного излучения, возникающего в таких трубках. В наши дни атомы часто возбуждают лазерным излучением.
Метод молекулярных пучков.
Особенно простой, показательный и прямой метод измерения атомных магнитных моментов предложили О.Штерн и В.Герлах в 1921. Он основан на измерении отклонения атомов, обладающих магнитным моментом, в неоднородном магнитном поле. В однородном магнитном поле магнитный момент не отклоняется, т.к. на северный и южный полюса атомного магнитика поле действует с одинаковой силой. Поэтому центр масс атома не смещается; атом может лишь прецессировать или вращаться вокруг своего центра масс. Если же магнитное поле неоднородно на расстояниях порядка размеров атома, то из-за различий в напряженности магнитного поля на один из полюсов атомного магнитика поле будет действовать сильнее, чем на другой, и атом отклонится под действием разности этих сил.
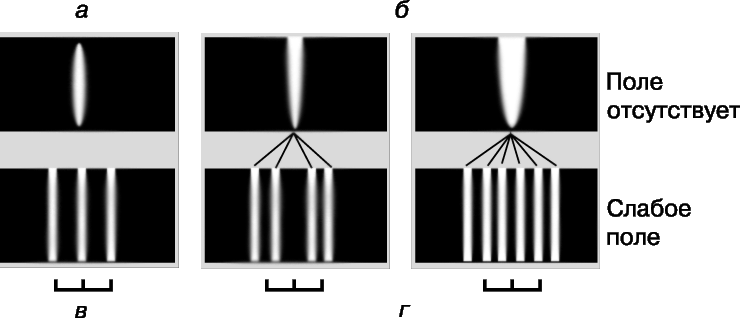
В эксперименте материал нагревается в печи и его атомы через щель проходят в вакуумную камеру, где коллимируются в пучок и осаждаются на пластинке. Затем включается неоднородное магнитное поле, направленное поперек пучка, и регистрируется отклонение атомов. Каждому из возможных значений проекции магнитного момента и спина на направление поля должно соответствовать свое отклонение. Соответствующее классической физике непрерывное распределение проекций привело бы к сплошному размытию сигнала на регистрирующей пластинке. Но в квантовой механике допустимы лишь определенные дискретные проекции, и поэтому наблюдаемая картина расщепляется на две или несколько линий, число которых равно 2j + 1, где j – момент импульса атома в указанных выше единицах. По числу компонент 2j + 1 можно определить момент импульса – спин j. Расстояние между линиями позволяет вычислить величину магнитного момента.
Для измерения атомных магнитных моментов были приспособлены также рассматриваемые ниже резонансные методы молекулярных пучков, и они дали наиболее точные результаты. Точно так же для измерения атомных магнитных моментов применяется метод электронного парамагнитного резонанса, подобный методу ЯМР.
Выводы из опытов по определению атомных моментов.
Результаты упомянутых выше и других аналогичных экспериментов согласуются со следующими утверждениями относительно спиновых и магнитных моментов атомных структур.
Каждый элемент в атоме имеет соответствующий его движению по беровской орбите орбитальный момент l. Это движение электрона по орбите можно рассматривать как круговой ток, в результате чего возникает магнитный момент, соответствующий такому движению.
Величина магнитного момента, связанного с орбитальным движением, в классической механике была бы пропорциональна величине орбитального момента. Но у электрона есть еще и собственный момент – спин. Со спином также должен быть связан магнитный момент.
В результате магнитный момент частицы оказывается пропорционален полному механическому моменту (сумме орбитального и спинового моментов).
Важно иметь в виду, что моменты – механические и магнитные – векторные величины. В квантовой механике разработаны определенные способы их суммирования и вычисления магнитных моментов атомов.
ЯДЕРНЫЕ МОМЕНТЫ
Существует ряд методов измерения ядерных моментов; ниже обсуждаются некоторые из них.
Оптическая спектроскопия.
Один из наиболее важных методов измерения ядерных моментов основан на изучении так называемой сверхтонкой структуры атомных спектров, для возбуждения которых в настоящее время часто используют лазеры. Значение спина можно определить по числу компонент спектральных линий или по относительной интенсивности линий. Спин, магнитный момент и электрический квадрупольный момент можно определить по расстоянию между компонентами или по влиянию магнитного поля на линии. Спин можно также определять по полосатым спектрам двухатомных молекул.
Методы молекулярных пучков.
Методы молекулярных пучков, разработанные О.Штерном, И.Раби, Н.Рамзеем, У.Ниренбергом и другими исследователями, особенно эффективны при исследовании ядерных моментов. Известен ряд методов молекулярных пучков. В одном из них, применявшемся Штерном для измерения ядерных моментов водорода и дейтерия, использовались молекулярный водород и установка, в принципе сходная с установкой в опыте Штерна и Герлаха. Поскольку в молекулярном водороде магнитные моменты электронов почти точно компенсируют друг друга, наблюдаемое отклонение обусловлено, главным образом, магнитным моментом ядра. Поэтому измеренное отклонение позволяло определить ядерный магнитный момент. В экспериментах с пучками, проведенных Раби с сотрудниками, использовались атомы с отличным от нуля электронным магнитным моментом, из которых формировался атомный пучок, пропускавшийся через один или два отклоняющих магнитных поля такого же типа, как в опыте Штерна – Герлаха. Путем подбора магнитных полей и исследования картины отклонения или перефокусировки пучка атомов удалось получить сведения о связи ядерных и электронных моментов. Таким путем удалось измерить спины ядер, а также характеристики взаимодействия ядерных магнитных моментов и электрических квадрупольных моментов.
Наиболее эффективным методом изучения ядерных моментов, по-видимому, следует считать измерение поглощения атомами и молекулами электромагнитного излучения радиочастотного и микроволнового диапазонов. Как и в оптической спектроскопии, поглощение излучения молекулой происходит на частоте n, отвечающей значению hn = DE, где DE – разность энергий двух состояний, соответствующих разрешенному переходу. В случае простого магнитного момента m ядра со спином I, находящегося в магнитном поле Н, величину DE можно вычислить теоретически, и оказывается, что резонанс происходит на частоте n, такой, что hn = mH/I, где m – магнитный момент ядра. В этом соотношении h – постоянная Планка, а поэтому, измерив H и n, можно найти отношение магнитного момента к спину. Если же взаимодействие в молекуле оказывается более сложным, то равенство величин DE и mH/I нарушается и поглощение излучения происходит на частотах, отличающихся от соответствующих равенству hn = mH/I. Дополнительное взаимодействие может иметь место в случае ядра, обладающего электрическим квадрупольным моментом, т.к. этот момент может взаимодействовать с неоднородным электрическим полем, создаваемым зарядами других атомов молекулы, в состав которой входит ядро. В этом случае частоты, на которых происходит поглощение, позволяют определить электрический квадрупольный момент ядра.
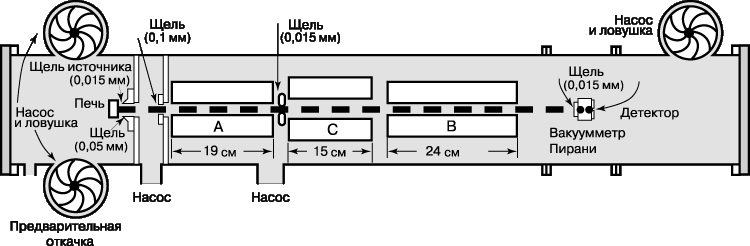
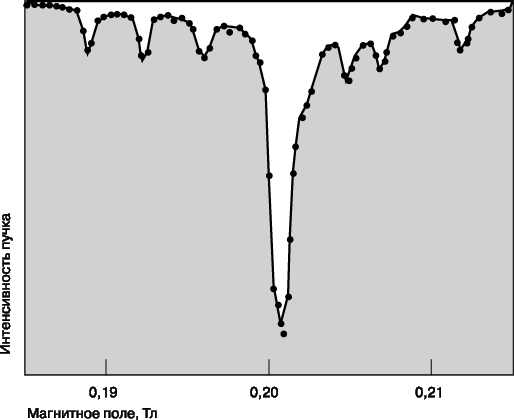
Описанный выше метод, основанный на поглощении радиочастотного излучения, впервые был успешно применен в 1937 И.Раби с сотрудниками и получил название метода магнитного резонанса на молекулярных пучках. Для регистрации факта поглощения Раби исследовал влияние поглощения на отклонение молекул в молекулярных пучках. Схема его экспериментальной установки приведена на рисунке. Молекулы из «печи» (термического источника) попадают в вакуумную камеру, в которой имеются магниты А и В, создающие неоднородные магнитные поля, направления неоднородностей который противоположны. В магните А молекулы отклоняются так, как это происходит в опыте Штерна и Герлаха, а затем перефокусируются магнитом В на детекторе при условии, что входящие в состав молекулы магнитные моменты одинаково ориентированы в А и В. Но если один из моментов переориентируется в средней области С, то перефокусировка не происходит и интенсивность пучка уменьшается. Поэтому в области С создают однородное магнитное и осциллирующее радиочастотное поля и измеряют поглощение радиочастотного излучения, регистрируя уменьшение интенсивности пучка. Типичные результаты эксперимента, проведенного с молекулами тяжелого водорода, представлены на рисунке. Это – зависимость интенсивности пучка от напряженности однородного магнитного поля в области С. Самый глубокий центральный минимум интенсивности пучка соответствует частоте n и напряженности поля H, которые связаны соотношением hn = mH/I (см. выше), так что эти данные позволяют определить отношение магнитного момента к спину. Менее глубокие дополнительные минимумы обусловлены электрическим квадрупольным моментом; по их положению можно определить электрический квадрупольный момент ядра тяжелого водорода, или дейтрона. Рамзей показал, что более высокой точности в измерении резонансных частот удается достичь, если создавать осциллирующие поля в двух узких промежутках – в начале и конце области С.
Для изучения полярных молекул Раби и его сотрудники применили метод электрического резонанса на молекулярных пучках не с магнитными, а с электрическими отклоняющими, перефокусирующими и осциллирующими полями. Этот метод оказался особенно ценным для исследования взаимодействия ядерных электрических квадрупольных моментов.
Ядерный магнитный резонанс (ЯМР).
В 1946 Э.Парселл и Ф.Блох с сотрудниками впервые успешно применили метод магнитного резонанса, при котором не используется молекулярный пучок, но наблюдается резонансное поглощение радиочастотного излучения в образце. Парселл регистрировал непосредственно поглощение излучения, тогда как Блох использовал пару ортогональных катушек: колебания на резонансной частоте, происходившие в одной из катушек, вызывали в образце переориентацию ядер, прецессия которых индуцировала в другой катушке наблюдаемый сигнал.
А.Кастлер и другие экспериментаторы получили значительно более сильные атомные резонансные сигналы, изменяя распределение ориентации ядер посредством оптической накачки и регистрируя резонанс по изменению интенсивности и поляризации испускаемого света.
Поскольку ЯМР-резонансы чрезвычайно узки, их положение можно измерить с очень высокой степенью точности, что, однако, не повышает сразу же точность измерения магнитного момента ядра, т.к. существует магнитное экранирование, создаваемое окружающими молекулами и вызывающее так называемый химический сдвиг резонанса. Н.Рамзей вывел общее теоретическое выражение для химических сдвигов и выполнил приближенные вычисления для большого числа молекул. Однако точность таких вычислений, как правило, ниже точности резонансных измерений. Хотя это обстоятельство является недостатком с точки зрения точного измерения магнитных моментов ядер, благодаря ему метод ЯМР нашел свое самое важное применение – в химии. Поскольку относительные химические сдвиги можно определить экспериментально и, кроме того, они заметно зависят от типа молекулы и расположения в ней ядра, точные измерения резонансных частот оказались мощным средством химического анализа. Из-за узости ЯМР-резонансов и необходимости использования сильных магнитных полей неизвестные магнитные моменты труднее определять методом ЯМР, чем методом молекулярных пучков. Поэтому большинство магнитных моментов ядер были впервые обнаружены и измерены методом молекулярных пучков, хотя позднее многие резонансы были измерены с большей точностью методом ЯМР. См. также ХИМИЯ АНАЛИТИЧЕСКАЯ; СПЕКТРОСКОПИЯ.
Другие методы.
Некоторые ядерные моменты определялись методами радиоспектроскопии: ионы захватываются электрическими и магнитными полями, после чего измеряются их магнитные моменты и константы внутренних взаимодействий. Такие методы оказались особенно эффективными с появлением методики лазерного охлаждения, позволившей охлаждать ионы до температур в несколько микрокельвинов, при которых ничтожно малы доплеровские эффекты уширения линий первого и второго порядков. Особенно важный пример – измерения магнитного момента электрона, проведенные Х.Демельтом и его сотрудниками. Эти измерения дали значение
me = 1,001159652193(10)m0,
которое согласуется с предсказаниями квантовой электродинамики в пределах 10 знаков после запятой.
В настоящее время имеется также возможность захвата и лазерного охлаждения нейтральных атомов, которые затем используются для точных измерений.
Результаты измерений.
С точки зрения теории ядра заслуживают внимания следующие результаты.
Магнитные моменты протона 1H1 и нейтрона 0n1 отличаются от ядерного магнетона, хотя исходное предсказание заключалось в том, что первый должен быть точно равен ядерному магнетону, а второй – нулю.
Разность магнитного момента дейтрона 1H2 и суммы магнитных моментов протона и нейтрона хотя и мала, имеет конечное значение. Это означает, что моменты протона и нейтрона в дейтроне аддитивны лишь приблизительно.
Магнитный момент 1H3 отличается от магнитного момента протона на 6,6%, хотя теоретически они должны быть равны.
У дейтрона имеется электрический квадрупольный момент, т.е. он отклоняется от сферической симметрии (имея форму мяча для игры в регби), тогда как теоретически предсказывалось, что он должен был бы обладать сферической симметрией.
Измеренный магнитный момент электрона согласуется с предсказанным квантовой электродинамикой вплоть до десятого знака после запятой. См. также ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ; МАГНИТНЫЙ РЕЗОНАНС; МАГНИТЫ И МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА; МЕХАНИКА; КВАНТОВАЯ МЕХАНИКА; СПЕКТР; СПЕКТРОСКОПИЯ.
ЯДЕРНЫЕ МОМЕНТЫ
| ЯДЕРНЫЕ МОМЕНТЫ | |||
| Ядро | Спин (в ед. h/2p ) |
Магнитный момент (в ядерных магнетонах) |
Квадрупольный момент* (в ед. 10–24 см2) |
| 0n1 | 1/2 | –1,9131 | 0 |
| 1H1 | 1/2 | 2,7927 | 0 |
| 1H2 | 1 | 0,8574 | 0,00282 |
| 1H3 | 1/2 | 2,9788 | 0 |
| 2He3 | 1/2 | –2,1275 | 0 |
| 2He4 | 0 | 0 | 0 |
| 3Li6 | 1 | 0,8220 | |
| 3Li7 | 3/2 | 3,2563 | |
| 4Be9 | 3/2 | –1,1774 | 0 |
| 5Be10 | 3 | 1,8008 | 0,06 |
| 5Be11 | 3/2 | 2,6885 | 0,0355 |
| 6C12 | 0 | 0 | 0 |
| 6C13 | 1/2 | 0,7024 | 0 |
| 6C14 | 0 | 0 | 0 |
| 7N14 | 1 | 0,4037 | 0,02 |
| 7N15 | 1/2 | –0,2831 | 0 |
| 8O16 | 0 | 0 | 0 |
| 8O17 | 5/2 | –1,8937 | –0,026 |
| 8O18 | 0 | 0 | 0 |
| * Нулевые значения – теоретические. | |||
Тригг Дж. Физика XX века: ключевые эксперименты. М., 1978
Акоста В. и др. Основы современной физики. М., 1981
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. М., 1989
Ответь на вопросы викторины «Физика»