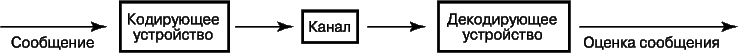ИНФОРМАЦИИ ТЕОРИЯ

Содержание статьи

• Кодирование.
• Сложность по Колмогорову.
• Каналы связи.

ИНФОРМАЦИИ ТЕОРИЯ – раздел математики, исследующий процессы хранения, преобразования и передачи информации. В основе его лежит определенный способ измерения количества информации. Возникшая из задач теории связи, теория информации иногда рассматривается как математическая теория систем передачи информации. Опираясь на основополагающую работу К.Шеннона (1948), теория информации устанавливает основные границы возможностей систем передачи информации, задает исходные принципы их разработки и практического воплощения. В настоящей статье рассматривается ядро теории информации – свойства информационных мер и их приложения к анализу систем передачи информации.

Основные свойства информации можно описать с помощью математической модели, отражающей многие характерные особенности информационной меры, как она обычно понимается на интуитивном уровне. Источник информации и канал связи, по которому передается информация, можно моделировать, используя вероятностные представления. Энтропия источника информации равна логарифму (эффективного) числа сообщений, которые он порождает. Это – мера сложности описания источника (или, как иногда говорят, мера неопределенности сообщения). Такое понимание энтропии тесно связано с понятием энтропии, используемым в термодинамике (см. также ТЕРМОДИНАМИКА).

Физически передачу информации можно представить как индуцирование в приемном устройстве требуемого физического состояния. Отправитель намерен передать сообщение получателю. Суть передачи заключается в воспроизведении на выходе канала связи переданного сообщения. В момент передачи отправитель выбирает нужное сообщение из списка всех возможных сообщений. Получатель заранее не знает, какое из них будет выбрано. (Если бы он был об этом заранее информирован, то никакой необходимости посылать сообщение не было бы.) Канал связи вносит в процесс передачи информации случайный шум, который искажает сообщение и тем самым затрудняет его прочтение. В начале процесса связи получатель находится в полной неопределенности относительно того, какое сообщение выбрано из списка возможных. К концу связи получателю становится это известно, т.е. становится известно точное описание выбранного сообщения.

Способность канала связи передавать информацию характеризуется некоторым числом – пропускной способностью (емкостью), равной логарифму эффективного числа сообщений, различимых на его выходе. Процесс передачи информации можно считать надежным, если скорость передачи сообщений меньше пропускной способности канала. В противном случае надежная передача информации оказывается невозможной. Основной результат теории информации состоит в утверждении: если энтропия источника меньше пропускной способности канала, то на его выходе исходное сообщение может быть воспроизведено со сколь угодно малой ошибкой; если же энтропия источника превышает его пропускную способность, то ошибку сделать малой невозможно.

Трудность передачи сообщения не зависит от его содержания; передавать бессмысленные сообщения не менее трудно, чем осмысленные. Например, число 23 в одном контексте может быть ценой одного барреля нефти, а в другом – номером победителя заезда на скачках. Смысл сообщения зависит от контекста и семантики, а трудность его передачи определяется только перечнем возможных сообщений (и их вероятностей).

Любую систему передачи информации можно считать состоящей из трех частей: источника сообщений, канала связи и приемного устройства (рис. 1). Например, при разговоре по телефону источником является говорящий, сообщением – его речь. Каналом связи служат провода, передающие электрический сигнал от говорящего к слушателю – получателю сообщения.

Между отправителем сообщения и каналом связи могут находиться устройства (обозначенные на рис. 1 как кодирующие), преобразующие сообщение в форму, удобную для передачи по каналу связи. Декодирующее устройство, установленное на другом конце канала, восстанавливает принятое сообщение.

Изучение систем передачи информации мы начнем с источника сообщений. По каналу связи может передаваться самая различная информация: текст, живая речь, музыка или изображения. Для каждого источника можно указать перечень сообщений, которые он может генерировать. Например, источник телеграфных или телексных сообщений передает только буквы и не содержит, скажем, нотных знаков. Если по каналу связи передается живая речь, то сигнал лишается полезного содержания при частоте выше 20 000 Гц, верхнего предела, воспринимаемого человеческим слухом. Этими фактами можно воспользоваться при проектировании входа канала связи.

Кодирование.

Моделью источника информации может служить генератор последовательности случайных величин. Следовательно, генерируемые сообщения можно рассматривать как исходы некоторого случайного испытания, вроде бросания игральной кости. Первоначально мы будем предполагать, что список возможных сообщений и их вероятности известны.

Трудность передачи информации зависит от числа возможных сообщений, которые должны быть распознаны получателем. Если это число невелико, то процесс передачи менее сложен, чем при большом числе возможных сообщений. Например, чтобы различить десять возможных сообщений, необходимо передать только одну десятичную цифру (0, 1, 2, .., 9), а для различения 100 возможных сообщений понадобятся уже две десятичные цифры (00, 01, 02, .., 99). Каждая дополнительная цифра позволяет увеличить число распознаваемых сообщений в 10 раз. Таким образом, количество информации, необходимой для того, чтобы мы могли различить N сообщений, растет, если говорить на математическом языке, как логарифм числа N, т.е. как log N.

Простейший список возможных сообщений состоит из двух сообщений. Чтобы передать одно из них, необходим символ, принимающий два значения. Количество информации, которую может передать источник, содержащий два равновероятных сообщения, называется битом и служит основной единицей измерения информации. Символ, представляющий такое количество информации, обычно является двоичной цифрой, 0 или 1. Один бит позволяет различать две равновероятные возможности (0, 1), два бита позволяют различать четыре возможности (00, 01, 10, 11), и т.д. Если число равновероятных возможностей равно N, то количество информации, необходимое для представления одной из них, равно log₂N битов. Например, чтобы передать одно из 32 возможных сообщений, отправитель мог бы послать получателю последовательность из log₂32 = 5 битов. Эта последовательность из 5 двоичных знаков сообщит получателю, какое из 32 возможных сообщений было передано.

Другой подход к той же проблеме можно пояснить на примере игры в 20 вопросов. Один из участников игры задумывает нечто, а другой пытается это отгадать с помощью 20 вопросов, допускающих ответы только типа «да – нет». Предположим, например, что первый из участников игры задумывает «Чарлз Диккенс». Второй участник игры может задать вопрос: «Это реальное лицо?», а затем спросить: «Этот человек жив?» и т.д. С каждым вопросом число вариантов отгадки уменьшается до тех пор, пока задуманное не будет идентифицировано. На языке теории информации можно сказать, что второй участник игры (отгадывающий задуманное) с каждым вопросом может получать самое большее один бит информации. С помощью 20 вопросов он может различить самое большее 2²⁰ (т.е. приблизительно миллион) различных объектов.

Если второй участник игры задает свои вопросы не слишком задумываясь, то ему скорее всего понадобится их гораздо больше. Например, чтобы идентифицировать один объект из миллиона возможных, может потребоваться миллион вопросов типа «Задуманный объект – это x?» Чтобы максимально использовать задаваемые вопросы, каждый вопрос должен делить множество возможных ответов примерно на две равные части. Тогда после первого вопроса останется только 500 000 возможных ответов, после второго – только 250 000, и т.д., пока, наконец, после 20-го вопроса не останется только один возможный ответ. Таким образом, в случае N равновероятных сообщений для выбора сообщения требуется около log N битов, а в игре в 20 вопросов для идентификации задуманного объекта требуется log N вопросов, допускающих ответы типа «да - нет».

Если заранее известно, что первый участник игры более чем в половине случаев задумывает «Уильяма Шекспира», то имеет смысл, задавая первый вопрос, спросить: «Это Уильям Шекспир?» Более чем в половине случаев отгадка будет найдена с помощью одного вопроса, и поэтому в среднем число вопросов окажется меньше, чем в описанной выше процедуре. Таким образом, если возможные ответы не равновероятны, то для идентификации наиболее вероятных кандидатов разумнее использовать более короткие последовательности вопросов (и, соответственно, более длинные для идентификации менее вероятных кандидатов).

Точно также и не всегда равновероятны сообщения, порождаемые источниками информации. Если одно сообщение имеет намного более высокую вероятность, чем другие, то для его идентификации мы можем использовать более короткое представление и более длинные – для других, менее вероятных. Предположим, например, что источник генерирует одно из четырех сообщений A, B, C и D с вероятностями ¹/₂, ¹/₄, ¹/₈ и ¹/₈. Каждое сообщение из этого списка можно было бы представить кодовым словом в два бита (например, представить A кодовым словом 00, B – кодовым словом 01, C – кодовым словом 10 и D – кодовым словом 11). Средняя длина такого представления составляет два бита. Мы могли бы также представить сообщение A кодовым словом 0, B – кодовым словом 10, C – кодовым словом 110 и D – кодовым словом 111. Приняв на выходе некоторую последовательность битов, получатель может решить, какое из четырех сообщений было передано. Средняя длина такого представления равна (¹/₂ ×1) + (¹/₄×2) + (¹/₈×3) + (¹/₈×3) = 1,75 бита. Таким образом, представление с переменной длиной кодовых слов в среднем оказывается короче, и при его достаточно продолжительном использовании мы сэкономили бы биты (1,75 по сравнению с 2). В какой-то степени это согласование имеется уже в коде Морзе, где чаще встречающиеся буквы обозначаются более короткими комбинациями точек и тире. Минимальная средняя длина представления ограничена некоторой фундаментальной величиной, называемой энтропией источника.

Источник информации можно представить в виде случайной величины X, принимающей одно из конечного числа возможных значений {1, 2, ..., m} с вероятностью p_i (p_i – вероятность того, что X = i). Энтропия случайной величины X по определению равна

где логарифмы берутся по основанию 2 и энтропия измеряется в битах. Такое определение энтропии связано с определением энтропии в термодинамике. Энтропия устанавливает нижнюю границу средней длины любого двоичного представления случайной величины.

Рассмотрим случайную величину X, принимающую значения {a, b, c} с вероятностями (¹/₂, ¹/₄, ¹/₄). Код для этой случайной величины мог бы иметь вид (0, 10, 11). Увидев строку 01001110, получатель мог бы однозначно разбить ее на 0, 10, 0, 11, 10, что декодируется в строку {a, b, a, c, b}, причем необходимости в специальном символе для обозначения конца кодированного слова не возникает. Заметим, что средняя длина такого кода составляет (¹/₂ ×1) + (¹/₄ ×2) + (¹/₄ ×2) = 1,5 бита, т.е. совпадает с энтропией источника.

Так же, как мы определили энтропию одной случайной величины, можно определить энтропию последовательности, или множества, случайных величин. Коэффициент энтропии такой последовательности равен пределу отношения энтропии последовательности к числу элементов этой последовательности и называется энтропией сообщения на символ. Если случайные величины коррелированы, то энтропия последовательности меньше суммы энтропий ее элементов.

Один из основных результатов теории информации связан с теоремой, согласно которой выборочную случайную величину можно представить без ошибки с помощью H + 1 бита и невозможно представить источник без ошибки с помощью менее, чем H битов. Отсюда следует, что энтропия является фундаментальным ограничением для представления источника информации, и мы можем найти представления со средней длиной в пределах одного бита энтропии. Оптимальное представление случайной величины (в терминах средней длины) может быть найдено с помощью алгоритма Хаффмана. Этот алгоритм позволяет строить коды для источников с энтропией, не превышающей одного бита.

Теоретически можно вычислить коэффициент энтропии случайного процесса, моделирующего источник информации, а затем найти представления, не превышающие один бит энтропии. Однако многие встречающиеся на практике источники информации обладают структурой, которую очень трудно представить в рамках простой модели. Примером источника, который исследовали многие авторы, служит английский текст. Попытаемся оценить коэффициент энтропии английского языка с помощью различных моделей.

Для простоты предположим, что английский алфавит состоит из 26 букв и одного пробела. В простейшей модели все знаки равновероятны. Можно показать, что энтропия такой модели равна log 27 = 4,76 бита на букву. Но в реальном английском языке буквы не равновероятны (например, буква E встречается с большей вероятностью, чем Q). Используя относительные частоты различных букв для вычисления энтропии, мы получили бы оценку около 4,03 бита на букву. Таков был бы коэффициент энтропии, если бы буквы английского алфавита встречались независимо друг от друга.

Но это не так. Например, за буквой Q почти всегда следует U, и т.д. Воспользовавшись условными распределениями, мы могли бы построить более точную оценку коэффициента энтропии английского языка. Например, если воспользоваться моделью, в которой каждая буква зависит только от предыдущей, то получится оценка примерно в 3,3 бита на букву. Рассматривая распределение букв, которое зависит от трех предыдущих букв, мы получаем оценку примерно в 2,8 бита на букву.

Однако всю сложность зависимостей, существующих в реальном английском языке, ни одна из этих моделей полностью не передает. Зато играя в игру, аналогичную игре в 20 вопросов, и состоящую в угадывании следующей буквы, можно получить гораздо более точные оценки коэффициента энтропии английского языка. Эксперименты с образцами английских текстов показывают, что коэффициент энтропии немного больше, чем 1 бит на букву. Это означает, что в английском языке существует значительная избыточность, которую можно устранить с помощью подходящего кодирования. Например, не составляет никакого труда декодировать следующее английское предложение:

TH... ...R... ...S ...NLY ...N... W...Y

T...  F...LL ...N TH... V...W...LS

...N TH...S S...NT...NC... .

IS ONLY ONE WAY

FILL IN THE VOWELS

THIS SENTENCE,

хотя почти половина букв отсутствует. Как показывают оценки коэффициента энтропии, английский язык, вообще говоря, допускает примерно четырехкратное сжатие, если воспользоваться для этого идеальным сжимающим алгоритмом. Например, 300-страничное издание Повести о двух городах Чарлза Диккенса можно было бы сократить до объема в 75 страниц такой же печати. Разумеется, в сжатом варианте буквы алфавита от A до Z использовались бы примерно одинаковое число раз, поэтому сжатый текст мог бы выглядеть, как «ZQRRLEWј». Тем не менее механизм «растяжения» позволил бы восстановить первоначальный текст Повести о двух городах слово в слово.

Непосредственное применение алгоритма Хаффмана для нахождения оптимального кода требует знания характерного для данного источника информации распределения вероятностей. Однако во многих случаях, как и в примере с английским языком, распределение вероятностей либо неизвестно, либо слишком сложно для того, чтобы его можно было использовать для кодирования. Но и в этих случаях можно придумать такие алгоритмы, которые восстанавливают распределение вероятностей по эмпирическим данным, а затем используют полученную информацию для сжатия данных. Такие алгоритмы называются универсальными. Широко известным примером может служить алгоритм Лемпеля – Зива, который не требует знания статистики источника информации и тем не менее асимптотически оптимален (см. ниже). Основная идея заключается в составлении словаря или таблицы, часто встречающихся фраз и в представлении новых фраз по их префиксам в таблице. Последовательность букв прежде всего необходимо разбить на последовательности, не встречавшиеся ранее. Например, двоичную строку 11010011011100 мы разбиваем на последовательности 1, 10, 100, 11, 0, 111, 00. Затем вместо того, чтобы передавать биты каждой фразы, мы передаем указатель фразы и значение ее последнего бита. Например, если мы используем для указателя три бита, то нашу исходную строку представляем последовательностью (000, 1), (001, 0), (010, 0), (001, 1), (000, 0), (100, 1), (101, 0) и т.д. Самое удивительное заключается в том, что, как показали А.Лемпель и Я.Зив, для всех «хороших» источников информации их алгоритм асимптотически оптимален в смысле сходимости коэффициента сжатия к энтропии. Таким образом, для всех достаточно длинных массивов алгоритм Лемпеля – Зива (не требующий никаких допущений относительно распределения вероятностей источника) позволяет достичь таких же результатов, как если бы мы заранее знали вероятностное распределение и построили для него оптимальный код.

Описанный алгоритм – лишь один из широкого класса аналогичных адаптивных алгоритмов, действующих на основе словаря и называемых алгоритмами Лемпеля – Зива. Они просты, обладают высоким быстродействием и реализуются как с помощью программного обеспечения, так и аппаратно. Их используют, чтобы «удвоить» емкость памяти для хранения данных или эффективную скорость передачи модема, поскольку в большинстве случаев они позволяют вдвое сжать английские тексты.

Сложность по Колмогорову.

В 1960-х годах русский математик А.Н.Колмогоров поставил вопрос: «Какова внутренняя сложность описания строки двоичных символов?» Если двоичную строку рассматривать как последовательность независимых и одинаково распределенных случайных величин, то в среднем для ее описания нам понадобилось бы число битов, равное энтропии последовательности. Но что если бы двоичными символами были двоичные цифры, составляющие миллион первых знаков двоичного разложения числа p? В этом случае строка символов кажется случайной, но ее можно получить с помощью простой компьютерной программы. Поэтому если бы мы захотели переслать миллионы битов такой строки куда-нибудь в другое место, где имеется компьютер, то могли бы вместо двоичных знаков переслать программу и попросить компьютер на месте воспроизвести заново эти миллионы битов. Таким образом, сложность описания миллиона битов разложения числа p очень мала.

Исходя из такого рода соображений, А.Н.Колмогоров определил сложность двоичной строки как длину кратчайшей программы для универсального компьютера, способной генерировать эту строку. (Такое представление о сложности независимо и почти одновременно предложили Г.Чайтин и Р.Соломонофф.) Универсальный компьютер можно рассматривать как машину Тьюринга, которая может моделировать любой другой универсальный компьютер. На первый взгляд кажется, что предложенное А.Н.Колмогоровым определение сложности бесполезно, поскольку зависит от возможностей конкретного компьютера. Но это не так, поскольку любой универсальный компьютер может моделировать любой другой универсальный компьютер, то любая программа, написанная для одного компьютера, может быть конвертирована в программу для другого компьютера путем добавления в качестве префикса «программы имитации», имеющей постоянную длину. Опираясь на эту идею, можно показать, что величина сложности по существу не зависит от компьютера. Внутренняя сложность описания любого объекта не зависит от компьютера или лица, описывающего данный объект. При некоторых предположениях можно доказать, что сложность по Колмогорову есть не что иное, как шенноновская энтропия. Иначе говоря, в среднем длина кратчайшей компьютерной программы, способной воспроизвести случайный объект, равна энтропии вероятностного распределения, из которого этот объект был извлечен. Сложность по Колмогорову предлагает единый подход к проблемам сжатия данных. Кроме того, она служит основой теории статистических выводов (бритва Оккама: «Простейшее объяснение – лучшее») и тесно связана с теорией вычислимости.

Каналы связи.

До сих пор мы рассматривали сложность описания источника информации и показали, что естественной мерой этой сложности служит коэффициент энтропии случайного процесса, моделирующего источник. Рассмотрим теперь проблему передачи этого описания по каналу связи. Примерами каналов связи могут служить телеграфные и телефонные провода, передающие информацию посредством электрических сигналов. В сотовых телефонах информация передается с помощью электромагнитного излучения.

Вместо того, чтобы заниматься конкретными деталями той или иной системы связи, мы можем построить ее общую модель. Это делается заданием списков возможных входных и выходных символов, а также функции распределения вероятностей, указывающей вероятность различных возможных выходных символов для каждого возможного входного символа. В простейшем случае выходной сигнал канала равен входному сигналу, и любая поступающая на вход информация без ошибок передается на выход. Например, если бы у нас был канал, который мог бы передавать два символа, и оба они принимались на выходе без ошибки (рис. 2), то с каждым символом мы могли бы передавать один бит информации. Такие каналы получили название каналов без шума. Их пропускная способность равна максимальному количеству информации, которое может поступить на вход. Если канал имеет N возможных входных символов, то его пропускная способность равна log N битов за передачу. Если такой канал может передавать 1 символ в секунду, то его пропускная способность равна log N битов в секунду.

Однако в общем случае сигналы на входе и выходе канала связи не совпадают. Рассмотрим, например, изображенный на рис. 3 канал связи с двумя входами и двумя выходами. Входами для этого канала служат символы «0» или «1». Если передается «0», то на выходе получатель видит в 90% случаев «0», а в 10% символ «1», что составляет ошибку в 10%. Следовательно, передав по каналу длинную последовательность битов, мы получим на выходе последовательность, в которой 10% двоичных цифр будут ошибочными. Если бы получатель знал, какие знаки неверны, их можно было бы исправить, заменив 0 на 1 и наоборот. Однако, поскольку такой информации у него нет, он может знать значение первого переданного по каналу бита не более, чем с 90%-й уверенностью.

Степень уверенности получателя можно повысить, повторяя сообщение. Например, мы можем трижды повторить передачу первого бита. Взглянув на трижды полученные биты, тот, кому они предназначены, «по большинству голосов» решает, какой именно двоичный знак был ему передан. Ошибиться он может только в том случае, если неверными были два или более битов. Вычисляя вероятность такого события, мы приходим к заключению, что получатель на этот раз будет ошибаться в 2,8% случаев. Увеличивая число повторений, мы можем и далее снижать вероятность ошибки.

Однако для этого нам понадобится все больше и больше сообщений. В результате скорость передачи информации снизится: например, если мы использовали 9 сообщений для передачи 1 бита, то она составит ¹/₉ бита на передачу. До Шеннона инженеры-связисты полагали, что повторная передача сигнала – лучшее средство повышения ее надежности, т.е. для того, чтобы снизить вероятность ошибки, надо снизить скорость передачи информации. Но Шеннон в своей основополагающей статье показал, что снижать скорость передачи информации для этого совсем не обязательно. С каждым каналом связи связана некоторая критическая скорость передачи информации, называемая пропускной способностью, или емкостью, канала. Информацию можно передавать со сколь угодно малой вероятностью ошибки и с любой скоростью, если она меньше критической. Для скоростей, превышающих пропускную способность канала, вероятность ошибки не может быть малой, более того, с ростом длины используемого кода она приближается к 1.

В приведенном выше примере двоичного канала его пропускная способность составляет 0,53 бита на передачу. Таким образом, с помощью 100-кратного повторения мы можем передать по этому каналу 53 бита информации с пренебрежимо малой вероятностью ошибки.

Поскольку теорема Шеннона о пропускной способности канала связи в чем-то противоречит нашей интуиции, попытаемся понять, почему эта теорема верна. Рассмотрим канал, изображенный на рис. 4. В этом канале существует 10 возможных входных символов, обозначенных цифрами 0, 1, 2, ј, 9, и десять возможных выходных символов. Каждый входной символ с равной вероятностью порождает выходной символ, обозначенный либо той же цифрой, либо на единицу больше. Например, цифра 3 на входе с равной вероятностью порождает на выходе 3 или 4, а цифра 9, соответственно, – 9 или 0. Поэтому, обнаруживая на выходе канала цифру 5, мы не можем однозначно утверждать, была ли передана цифра 5 или 4.

Если мы ограничим множество входных символов четными числами, т.е. 0, 2, 4, 6 и 8, то при любом выходном символе без всякой неопределенности или ошибки сможем указать соответствующий входной символ. Таким образом, используя лишь некоторое подмножество возможных входных символов, мы можем передавать информацию без ошибок. Скорость, с которой мы можем передавать информацию по этому каналу, равна log 5 битов на передачу. Можно показать, что эта скорость оптимальна и совпадает с пропускной способностью канала, изображенного на рис. 4.

Таким образом, если считать, что при передаче длинной последовательности символов все каналы подобны каналу, изображенному на рис. 4, то теорема Шеннона может выглядеть интуитивно более оправданной. Длинная последовательность входных символов может порождать любую выходную последовательность, но по законам теории вероятностей скорее всего породит одну из небольшого множества условно «типичных» выходных последовательностей. Например, в двоичном симметричном канале входная последовательность длины n вероятнее всего породит одну из 2^nH(p) условно типичных последовательностей (где H (p) = –p log p – (1 – p) log (1 – p) и p – вероятность того, что «0» будет принят как «1» или наоборот). Так как всего существует 2ⁿ возможных выходных последовательностей длины n, нетрудно показать, что можно выбрать ок. 2ⁿ/2^{nH (p)} = 2^{n(1 – H (p))} различных входных последовательностей (называемых кодовыми словами), таких, что их выходные варианты будут существенно неперекрывающимися (как на рис. 4), и, следовательно, получатель сможет различить эти последовательности с очень малой ошибкой. Таким образом, пропускная способность такого канала (скорость, с которой информация может быть передана по нему с пренебрежимо малой ошибкой) по существу равна 1 – H (p) битов на одну передачу.

В общем случае пропускная способность канала определяется разностью между безусловной энтропией выхода канала и условной энтропией канала с заданным входным сигналом. Эта величина называется взаимной информацией между входом и выходом канала; максимум взаимной информации по всем распределениям вероятностей входа является пропускной способностью канала. Если распределение вероятностей, которому подчиняется канал, известно, то эта величина может быть вычислена.

До сих пор мы рассматривали дискретные каналы связи. Это каналы, сигналы на входе и выходе которых представлены дискретными последовательностями символов. Однако во многих практически используемых устройствах передачи информации сигналы имеют вид непрерывно меняющихся функций времени. Важным примером здесь является гауссовский канал с заданной полосой пропускания, где параметры входного сигнала ограничены средней мощностью P ватт и спектром частот в некотором их диапазоне шириной W гц, а на выходе получается входной сигнал, искаженный шумом с плоским спектром частот, средней плотностью рассеиваемой мощности N ватт/гц и с гауссовым распределением вероятностей. В этом случае мы можем воспользоваться «теоремой отсчетов» и показать, что входной сигнал можно представить, взяв 2W его выборочных значений в секунду. Можно показать также, что пропускная способность такого канала определяется по формуле

Такой непрерывный канал служит полезной моделью многих широко используемых на практике каналов радио- и телефонной связи.

Коэффициент энтропии источника и пропускная способность канала связаны основной теоремой теории информации, которая гласит: кодирующие и декодирующие устройства, позволяющие безошибочно воссоздавать входной сигнал на выходе, могут быть построены в том и только в том случае, если коэффициент энтропии источника меньше пропускной способности канала. Теория информации ничего не говорит нам о том, как именно такие кодирующие и декодирующие устройства можно сконструировать, она лишь говорит о возможности их существования в принципе, если предположить, что их сложность может быть сколь угодно велика. Создание таких устройств составляет предмет теории кодирования, ставшей самостоятельной наукой со своими методами и важными результатами. Для создания практических кодирующих и декодирующих устройств были разработаны различные тонкие алгебраические методы. Широкому распространению таких кодов способствовали и успехи в развитии технологии интегральных схем. Например, в плейерах для проигрывания компакт-дисков используется один из видов кодов, исправляющих ошибки, который называется кодом Рида – Соломона и способен исправлять до 4000 следующих подряд ошибок.

Последние достижения в области теории информации несколько расширили понятия пропускной способности и сжатия данных на случай сетей каналов связи. Прогресс в теории кодирования позволил создавать модемы для телефонных каналов, вплотную приблизившие скорость передачи информации к их пропускной способности. Универсальные алгоритмы сжатия данных типа алгоритма Лемпеля – Зива ныне широко используются для сжатия компьютерных файлов. Теория информации остается активно развивающейся областью исследований, поставляющей в наш информационный век новые идеи и подходы в сферу проектирования и анализа систем передачи данных и компьютерных систем.